题目内容

16．已知数列{an}是等差数列，若a1-a9+a17=7，则a3+a15=（　　）
A．7B．14C．21D．7（n-1）

分析 利用等差数列的性质即可得出．

解答 解：∵数列{an}是等差数列，a1-a9+a17=7，
∴2a9-a9=7，可得a9=7．
则a3+a15=2a9=14．
故选：B．

点评 本题考查了等差数列的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
14．一个几何体按比例绘制的三视图如图所示，则该几何体的体积为（　　）
A．6B．7C．8D．9
15．已知随机变量ξ～B（n，p），且E（ξ）=12，D（ξ）=2.4，则n与p的值分别是（　　）
A．15，$\frac{4}{5}$B．18，$\frac{2}{3}$C．20，$\frac{3}{5}$D．24，$\frac{1}{2}$
4．已知函数f（x）=ex+ax2+bx+c，a，b，c∈R．
（1）若曲线y=f（x）在点（0，f（0））处的切线方程为3x-y+2=0，求b，c的值；
（2）若b=0，且f（x）在$[{\frac{1}{2}，+∞}）$上单调递增，求实数a的取值范围．
11．下列说法正确的是（　　）
A．命题“?x∈R，使得x2+x+1≥0”的否定是“?x∈R，使得x2+x+1≥0”
B．实数x＞y是x2＞y2成立的充要条件
C．设p，q为简单命题，若“p∨q”为假命题，则“￢p∧￢q”也为假命题
D．命题“若cosα≠1，则α≠0”为真命题
1．已知函数f（x）=ax2-x+a，a∈R，
（1）当a=2时，解不等式f（x）＞3；
（2）若函数f（x）有最大值-2，求实数a的值．
8．若m∈（4，7），则直线y=kx+k与圆x2+y2+mx+4=0至少有一个交点的概率是（　　）
A．$\frac{1}{5}$B．$\frac{2}{3}$C．$\frac{3}{5}$D．$\frac{1}{3}$
5．若△ABC的面积为S=a2-（b-c）2，则$\frac{sinA}{1-cosA}$=4．
6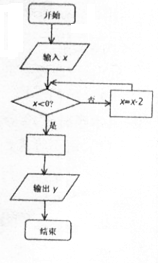．如图是一个算法程序框图，当输入的x的值为4时，输出的结果恰好是$\frac{1}{4}$，则空白处的关系式可以是（　　）
A．y=2-xB．y=2xC．y=x${\;}^{-\frac{1}{2}}$D．y=x${\;}^{\frac{1}{2}}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网