题目内容
5．若△ABC的面积为S=a2-（b-c）2，则$\frac{sinA}{1-cosA}$=4．分析 本题考查正弦定理，余弦定理以及任意三角形的面积公式．
解答 ：由S=a2-（b-c）2
∴S=a2-b2-c2+2bc
由任意三角形的面积公式S=$\frac{1}{2}bcsinA$和余弦定理：a2-b2-c2=-2bccosA
∴$\frac{1}{2}bcsinA$=2bc-2bccosA
解得：sinA=4-4cosA=4（1-cosA）
∴$\frac{sinA}{1-cosA}=\frac{4（1-cosA）}{1-cosA}$
∵1-cosA≠0
∴$\frac{sinA}{1-cosA}=4$
故答案为4．
点评 本题考查正弦定理，余弦定理以及任意三角形的面积公式的灵活运用能力和化简计算能力．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
16．已知数列{an}是等差数列，若a1-a9+a17=7，则a3+a15=（ ）
| A． | 7 | B． | 14 | C． | 21 | D． | 7（n-1） |
13．△ABC的三个内角分别记为A，B，C，若tanAtanB=tanA+tanB+1，则cosC的值是（ ）
| A． | -$\frac{\sqrt{2}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
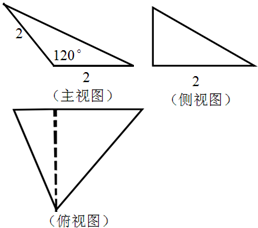某几何体的三视图如图，则该几何体的外接球表面积20π．