题目内容
14.一个几何体按比例绘制的三视图如图所示,则该几何体的体积为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由三视图可知:该几何体由三部分组成:最上面的是四棱锥,中间是一个长方体,下面是一个四棱台.
解答 解:由三视图可知:该几何体由三部分组成:最上面的是四棱锥,中间是一个长方体,下面是一个四棱台.
∴该几何体的体积V=$\frac{1}{3}×{2}^{2}×1$+2×12+$\frac{1}{3}×2×({2}^{2}+\sqrt{{2}^{2}×{1}^{2}}+{1}^{2})$
=8,
故选:C.
点评 本题考查了三视图、空间几何体的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
4.根据下列表格中的数据,可以断定方程ex-x-2=0的一个根所在的区间是(1,2).
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
5.设$\overrightarrow{a}$、$\overrightarrow{b}$是两个非零向量,则下列选项正确的是( )
| A. | 若|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | 若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | ||
| C. | 若|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$共线 | D. | 若$\overrightarrow{a}$,$\overrightarrow{b}$平行,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|, |
9.在平面直角坐标系xOy中,已知曲线C1:$\left\{\begin{array}{l}{x=1-t}\\{y=4-2t}\end{array}\right.$(t为参数)与曲线C2:$\left\{\begin{array}{l}{x=2+rcosθ}\\{y=1+rsinθ}\end{array}\right.$ (θ为参数,r>0)有一个公共点在y轴上,则r=( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
6.下列函数中,在[-1,0]上单调递减的是( )
| A. | y=cosx | B. | y=-|x-1| | C. | y=log${\;}_{\frac{1}{2}}}$$\frac{2-x}{2+x}$ | D. | y=ex+e-x |
16.已知数列{an}是等差数列,若a1-a9+a17=7,则a3+a15=( )
| A. | 7 | B. | 14 | C. | 21 | D. | 7(n-1) |
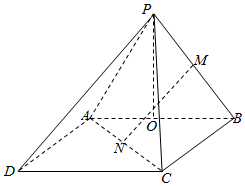 如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,
如图,已知底面为菱形的四棱锥P-ABCD中,△ABC是边长为2的正三角形,AP=BP=$\frac{\sqrt{2}}{2}$,PC=$\sqrt{2}$且N为线段AC的中点,M为侧棱PB的中点,O为线段AB的中点,