题目内容
12.某学校高二年级共有编号为1班,2班,3班,a,10班等10个班,每个班均有50个学生,现在需要用系统抽样的方法从每个班中抽取1人,得到一个容量为10的样本.首先,在给全体学生编号时,规定从1班到10班,各个学生的编号从小到大,即按1班从001到050,2班从051到100,3班从101到150,p,以此类推,一直到10班的50个学生编号为451到500.若用简单随机抽样的方法从1班抽到的编号为6号,则在6班中应抽取学生的编号为( )| A. | 12 | B. | 56 | C. | 256 | D. | 306 |
分析 根据已知计算出组距,可得答案
解答 解:因为是从500名学生中抽出10名学生,
组距是50,
∵从1班抽到的编号为6号,
∴在6班中应抽取学生的编号为6+5×50=256,
故选C.
点评 本题考查系统抽样的应用,是基础题,解题时要认真审题,注意熟练掌握系统抽样的概念

练习册系列答案
相关题目
20.在等差数列{an}中,a3+a4+a5+a6+a7=400,则a2+a8=( )
| A. | 40 | B. | 80 | C. | 160 | D. | 320 |
7.已知F1、F2分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的左右两个焦点,过F1作倾斜角为$\frac{π}{4}$的弦AB,则△F2AB的面积为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$-1 |
17.如图,OABC是四面体,G是△ABC的重心,G1是OG上一点,且OG=3OG1,则( )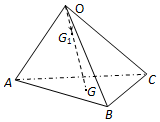

| A. | $\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$ | D. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$ |
1.若实数x,y满足$\left\{\begin{array}{l}3x-y-9≥0\\ x-y-3≤0\\ y≤3\end{array}\right.$,则使得z=y-2x取得最大值的最优解为( )
| A. | (3,0) | B. | (3,3) | C. | (4,3) | D. | (6,3) |
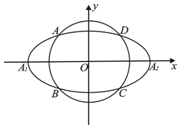 如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.
如图,椭圆C0:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,a,b为常数),动圆C1:x2+y2=t12,b<t1<a..点A1,A2分别为C0的左,右顶点,C1与C0相交于A,B,C,D四点.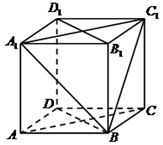 在正方体ABCD-A1B1C1D1中:
在正方体ABCD-A1B1C1D1中: