题目内容
6.某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表| 气温(°C) | 20 | 16 | 12 | 4 |
| 用电量(度) | 14 | 28 | 44 | 62 |
| A. | 70 | B. | 68 | C. | 64 | D. | 62 |
分析 由表格数据计算$\overline{x}$、$\overline{y}$,根据回归直线方程过样本中心点($\overline{x}$,$\overline{y}$)求出$\stackrel{∧}{a}$,
再写出回归方程,计算x=2时y的值即可.
解答 解:由表格数据得$\overline{x}$=$\frac{1}{4}$×(20+16+12+4)=13,
$\overline{y}$=$\frac{1}{4}$×(14+28+44+62)=37;
又回归直线方程y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中$\stackrel{∧}{b}$=-3,
且过样本中心点($\overline{x}$,$\overline{y}$),
所以37=-3×13+$\stackrel{∧}{a}$,
解得$\stackrel{∧}{a}$=76,
所以y=-3x+76;
当x=2时,y=-3×2+76=7,
即预测当气温为2℃时,用电量的度数是70(度).
故选:A.
点评 本题考查了回归直线方程过样本中心点的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设x,y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则(x+1)2+y2的最小值为( )
| A. | 1 | B. | $\frac{9}{2}$ | C. | 5 | D. | 9 |
17.如图,OABC是四面体,G是△ABC的重心,G1是OG上一点,且OG=3OG1,则( )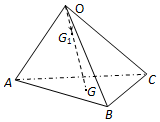

| A. | $\overrightarrow{O{G}_{1}}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$ | B. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$+$\frac{1}{3}$$\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G}_{1}}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{3}{4}$$\overrightarrow{OB}$+$\frac{3}{4}$$\overrightarrow{OC}$ | D. | $\overrightarrow{O{G}_{1}}$=$\frac{1}{9}$$\overrightarrow{OA}$+$\frac{1}{9}$$\overrightarrow{OB}$+$\frac{1}{9}$$\overrightarrow{OC}$ |
1.若实数x,y满足$\left\{\begin{array}{l}3x-y-9≥0\\ x-y-3≤0\\ y≤3\end{array}\right.$,则使得z=y-2x取得最大值的最优解为( )
| A. | (3,0) | B. | (3,3) | C. | (4,3) | D. | (6,3) |
18.等差数列{an}前n项和为Sn,公差d=-2,S3=21,则a1的值为( )
| A. | 10 | B. | 9 | C. | 6 | D. | 5 |
15.方程$lnx-\frac{1}{x}=0$的实数根的所在区间为( )
| A. | (3,4) | B. | (2,3) | C. | (1,2) | D. | (0,1) |
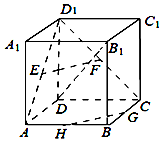 如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.
如图,已知正方体ABCD-A1B1C1D1,E,F,G,H分别是AD1、CD1、BC、AB的中点.