题目内容
方程a2•sin2x+asinx-2=0有解的条件是( )
| A、|a|≤1 | B、|a|≥1 |
| C、|a|≥2 | D、a∈R |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:通过换元法令z=asinx,得:z2+z-2=0,解出z的值,从而求出a的取值范围.
解答:
解:令z=asinx,
原方程可化为:z2+z-2=0,
解得:z=-2,或z=1,
于是:asinx=-2,sinx=-
,
∴|
|≤1,|a|≥2,
或者asinx=1,sinx=
,
∴|
|≤1,|a|≥1,
综上:|a|≥1,
故选:B.
原方程可化为:z2+z-2=0,
解得:z=-2,或z=1,
于是:asinx=-2,sinx=-
| 2 |
| a |
∴|
| 2 |
| a |
或者asinx=1,sinx=
| 1 |
| a |
∴|
| 1 |
| a |
综上:|a|≥1,
故选:B.
点评:本题考察了函数的根的存在性问题,三角函数的性质,渗透了换元思想,是一道基础题,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在复平面内,复数
对应的点位于( )
| 1-2i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
等差数列{an}中a1>0,S5=S8,则当Sn取最大值时n的值是( )
| A、6 | B、7 | C、6或7 | D、不存在 |
下面是一个2×2列联表,则a-b的值等于( )
| y1 | y2 | 总计 | |
| x1 | c | a | 69 |
| x2 | b | d | f |
| 总计 | e | 65 | 99 |
| A、45 | B、35 | C、34 | D、25 |
若数列{an}的前n项和Sn=3n2-10n,则数列的前10项中正数项的和为( )
| A、106 | B、208 |
| C、216 | D、118 |
设函数f(x)的导函数为f′(x),对任意x∈R,都有xf′(x)>f(x)成立,则( )
| A、3f(2)>2f(3) |
| B、3f(2)=2f(3) |
| C、3f(2)<2f(3) |
| D、3f(2)与2f(3)的大小不确定 |
要做一个圆锥形的漏斗,其母线长为40cm,要使其体积为最大,则高为( )
A、
| ||||
B、
| ||||
C、10
| ||||
D、
|
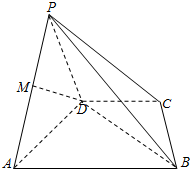 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.