题目内容
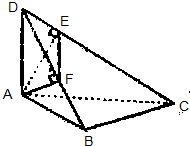 如图,在四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB,求证:
如图,在四边形ABCD中,DA⊥平面ABC,∠ABC=90°,AE⊥CD,AF⊥DB,求证:(1)EF⊥DC;
(2)平面DBC⊥平面AEF.
考点:平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据要证明线线垂直,只需要证线面垂直,要证线面垂直,需要证明线垂直面内的两条相交直线.
(2)先根据条件得到DA⊥BC进而得BC⊥平面DAB,把问题转化为证AF⊥平面DBC即可
(2)先根据条件得到DA⊥BC进而得BC⊥平面DAB,把问题转化为证AF⊥平面DBC即可
解答:
证明:(1) ∵DA⊥平面ABC,BC?平面ABC
∵DA⊥平面ABC,BC?平面ABC
∴DA⊥BC,
又BC⊥AB,AB∩AD=A
∴BC⊥平面ABD,
又AF?平面ABD,
∴BC⊥AF,
∵AF⊥DB,BC∩BD=B,
∴AF⊥平面BCD,
∵CD?平面BCD,
∴AF⊥CD,
∵AE⊥CD,AF∩AE=A
∴CD⊥平面AEF,
∵EF?平面AEF
∴CD⊥EF.
(2)由(1)可得AF⊥平面BCD
而AE?平面AEF
∴平面AEF⊥平面PBC
 ∵DA⊥平面ABC,BC?平面ABC
∵DA⊥平面ABC,BC?平面ABC∴DA⊥BC,
又BC⊥AB,AB∩AD=A
∴BC⊥平面ABD,
又AF?平面ABD,
∴BC⊥AF,
∵AF⊥DB,BC∩BD=B,
∴AF⊥平面BCD,
∵CD?平面BCD,
∴AF⊥CD,
∵AE⊥CD,AF∩AE=A
∴CD⊥平面AEF,
∵EF?平面AEF
∴CD⊥EF.
(2)由(1)可得AF⊥平面BCD
而AE?平面AEF
∴平面AEF⊥平面PBC
点评:本题主要考察面面垂直和线面垂直的判定,关键是它们之间的转化,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
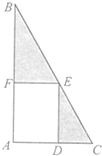 某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=
某学校计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形ADEF健身场地,如图,A=