题目内容
设a=log0.60.5,b=log2(log38),则( )
| A、b<1<a |
| B、a<b<1 |
| C、a<1<b |
| D、1<b<a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:利用对数函数的单调性即可得出.
解答:
解:∵a=log0.60.5>log0.60.6=1,b=log2(log38)<log2(log39)=log22=1,
∴a>1>b.
故选:A.
∴a>1>b.
故选:A.
点评:本题考查了对数函数的单调性,考查了推理能力,属于基础题.

练习册系列答案
相关题目
设复数z的共轭复数为
,若(2+i)z=3-i,则z•
的值为( )
. |
| z |
. |
| z |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
已知x0是函数f(x)=
在(0,+∞)上的一个极值点,则下面正确的结论是( )
| sinx |
| x |
A、tan(x0+
| ||||
B、tan(x0+
| ||||
C、tan(x0+
| ||||
D、tan(x0+
|
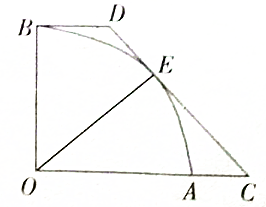 如图,扇形AOB的半径OA=2,∠AOB=
如图,扇形AOB的半径OA=2,∠AOB=