题目内容
设直线l的方程为(a+2)x+y-2-a=0(a∈R)
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与两坐标轴围成的面积是
,求直线l的方程.
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与两坐标轴围成的面积是
| 1 |
| 2 |
考点:直线的截距式方程
专题:直线与圆
分析:(1)若直线l经过原点,把(0,0)代入直线l的方程即可得出;若直线l不经过原点,即a≠-2,分别求出直线l在坐标轴上的截距即可得出;
(2)由(1)可得
|2+a|×1=
,解得a即可.
(2)由(1)可得
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)若直线l经过原点,则0-2-a=0,解得a=-2.∴直线l的方程为y=0;
若直线l不经过原点,即a≠-2,令x=0,解得y=2+a;令y=0,解得x=1.∴2+a=1,解得a=-1.此时直线l的方程为:x+y-1=0.
综上可得:直线l的方程为:y=0或x+y-1=0.
(2)由(1)可得
|2+a|×1=
,解得a=-1或-3.
∴直线l的方程为:x+y-1=0或x-y-1=0.
若直线l不经过原点,即a≠-2,令x=0,解得y=2+a;令y=0,解得x=1.∴2+a=1,解得a=-1.此时直线l的方程为:x+y-1=0.
综上可得:直线l的方程为:y=0或x+y-1=0.
(2)由(1)可得
| 1 |
| 2 |
| 1 |
| 2 |
∴直线l的方程为:x+y-1=0或x-y-1=0.
点评:本题考查了直线的截距式、分类讨论思想方法,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若关于x的不等式x2+ax-c<0的解集为{x|-2<x<1},对于任意的t∈[1,2],函数f(x)=ax3+(m+
)x2-cx在区间(t,3)上总不是单调函数,m的取什值范围是( )
| 1 |
| 2 |
A、-
| ||
| B、-3<m<-1 | ||
C、-
| ||
| D、-3<m<0 |
将函数y=cos(x+
)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向左平移
个单位,所得函数图象的一个对称中心为( )
| π |
| 3 |
| π |
| 3 |
| A、(0,0) | ||
B、(
| ||
C、(
| ||
| D、(π,0) |
已知O是坐标原点,点A(-2,1),若点M(x,y)为平面区域
上的一个动点,则
•
的取值范围是( )
|
| OA |
| OM |
| A、[0,1] |
| B、[0,2] |
| C、[-1,0] |
| D、[-1,2] |
设复数z的共轭复数为
,若(2+i)z=3-i,则z•
的值为( )
. |
| z |
. |
| z |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
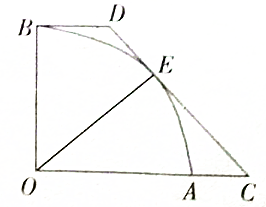 如图,扇形AOB的半径OA=2,∠AOB=
如图,扇形AOB的半径OA=2,∠AOB=