题目内容
14. 如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1,FC=2.
如图,已知ABCD是边长为2的正方形,EA⊥平面ABCD,FC∥EA,设EA=1,FC=2.(1)证明:EF⊥BD;
(2)求多面体ABCDEF的体积.
分析 (1)由地面ABCD是正方形,可得BD⊥AC,又EA⊥平面ABCD,可得BD⊥EA,然后利用线面垂直的判定得BD⊥平面EACF,最后可得EF⊥BD;
(2)把多面体ABCDEF的体积转化为2倍的棱锥B-ACFE的体积求解.
解答 (1)证明:∵ABCD是正方形,
∴BD⊥AC,
∵EA⊥平面ABCD,BD?平面ABCD,
∴BD⊥EA,
∵EA、AC?平面EACF,EA∩AC=A,
∴BD⊥平面EACF,
又∵EF?平面EACF,
∴EF⊥BD;
(2)解:∵ABCD是边长为2的正方形,
∴AC=$2\sqrt{2}$,
又EA=1,FC=2,
∴${S}_{ACEF}=\frac{1}{2}(1+2)•2\sqrt{2}=3\sqrt{2}$,
∴${V_{ABCDEF}}=2{V_{B-ACEF}}=2×\frac{1}{3}×{S_{ACEF}}×\frac{BD}{2}=4$.
点评 本题考查直线与平面垂直的判定与性质,考查了多面体体积的求法,训练了等积法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


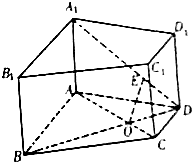 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.