题目内容
13.已知函数f(x)=$\sqrt{4+{x}^{2}}$,则?x1,x2∈R,x1≠x2,$\frac{|f({x}_{1})-f({x}_{2})|}{|{x}_{1}-{x}_{2}|}$的取值范围是[0,1).分析 ?x1,x2∈R,x1≠x2,$\frac{|f({x}_{1})-f({x}_{2})|}{|{x}_{1}-{x}_{2}|}$的取值范围,转化为利用导数求切线的斜率,即可得出.
解答 解:f′(x)=$\frac{x}{\sqrt{4+{x}^{2}}}$,
x=0时,f′(0)=0;
x>0时,f′(x)=$\frac{1}{\sqrt{\frac{4}{{x}^{2}}+1}}$∈(0,1);
x<0时,f′(x)=-$\frac{1}{\sqrt{\frac{4}{{x}^{2}}+1}}$∈(-1,0),
综上可得:f′(x)∈[0,1).
即?x1,x2∈R,x1≠x2,$\frac{|f({x}_{1})-f({x}_{2})|}{|{x}_{1}-{x}_{2}|}$的取值范围是[0,1).
故答案为:[0,1).
点评 本题考查了利用导数求切线的斜率、割线的斜率、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3.实数x,y满足$\left\{\begin{array}{l}{x+y-a≤0}\\{x-y≥0}\\{y≥0}\\{\;}\end{array}\right.$,若z=x-2y的最小值为-1,则实数a的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
18.若f(x)是定义在(-1,1)上的减函数,则下列不等式正确的是( )
| A. | f(sinx)>f(cosx) | B. | f($\frac{{x}^{2}+1}{2}$)>f(x) | ||
| C. | f($\frac{1}{{3}^{x}+1}$)≥f($\frac{1}{{2}^{x}+1}$) | D. | f($\frac{1}{{3}^{x}+{3}^{-x}}$)≥f($\frac{1}{{2}^{x}+{2}^{-x}}$) |
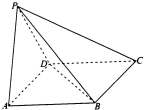 如图所示,四棱锥P-ABCD的底面是边长为a的菱形,∠DAB=60°,侧面PAD⊥底面ABCD,PA=PD.
如图所示,四棱锥P-ABCD的底面是边长为a的菱形,∠DAB=60°,侧面PAD⊥底面ABCD,PA=PD.