题目内容
18.关于下列命题:①函数y=tanx的一个对称中心是($\frac{π}{2}$,0);
②函数y=cos2($\frac{π}{4}$-x)是偶函数;
③函数y=4sin(2x-$\frac{π}{3}$)的一条对称轴是x=-$\frac{π}{12}$;
④函数y=sin(x+$\frac{π}{4}$)在闭区间[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数.
写出所有正确的命题的题号①③.
分析 由条件利用三角函数的图象和性质,得出结论.
解答 解:对于函数y=tanx,当x=$\frac{π}{2}$时,y无意义,故y=tanx的图象的一个对称中心是($\frac{π}{2}$,0),故①正确.
∵函数y=cos2($\frac{π}{4}$-x)=cos($\frac{π}{2}$-2x)=sin2x,故它是奇函数,故②错误;
令2x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,求得x=$\frac{kπ}{2}$+$\frac{5π}{12}$,可得函数y=4sin(2x-$\frac{π}{3}$)的一条对称轴是x=-$\frac{π}{12}$,故③正确;
在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上,x+$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3π}{4}$],函数y=sin(x+$\frac{π}{4}$)在闭区间[-$\frac{π}{2}$,$\frac{π}{2}$]上没有单调性,故④错误,
故答案为:①③.
点评 本题主要考查三角函数的图象和性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.某校高三文科600名学生参加了12月的模拟考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,将学生编号为000,001,002,…599
(Ⅰ)若从第6行第7列的数开始右读,请你依次写出最先抽出的5人的编号(下面是摘自随机数表的第4行至第7行);

(Ⅱ)抽出的100名学生的数学、外语成绩如表:
若数学成绩优秀率为35%,求m,n的值;
(Ⅲ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
(Ⅰ)若从第6行第7列的数开始右读,请你依次写出最先抽出的5人的编号(下面是摘自随机数表的第4行至第7行);

(Ⅱ)抽出的100名学生的数学、外语成绩如表:
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(Ⅲ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
3.实数x,y满足$\left\{\begin{array}{l}{x+y-a≤0}\\{x-y≥0}\\{y≥0}\\{\;}\end{array}\right.$,若z=x-2y的最小值为-1,则实数a的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
10.要做一个圆锥形漏斗,其母线长为30cm,要使其体积最大,则其高应为( )
| A. | 12$\sqrt{3}$cm | B. | 10$\sqrt{3}$cm | C. | 8$\sqrt{3}$cm | D. | 5$\sqrt{3}$cm |
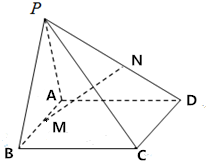 如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.
如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.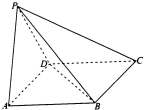 如图所示,四棱锥P-ABCD的底面是边长为a的菱形,∠DAB=60°,侧面PAD⊥底面ABCD,PA=PD.
如图所示,四棱锥P-ABCD的底面是边长为a的菱形,∠DAB=60°,侧面PAD⊥底面ABCD,PA=PD.