题目内容
14．将函数f（x）=sin（2x+φ）（0＜φ＜π）的图象向右平移2个单位后得到的函数图象关于原点对称，则实数φ的值为4-π．分析 由条件利用y=Asin（ωx+φ）的图象变换规律，正弦函数、余弦函数的图象的对称性，得出结论．
解答 解：将函数f（x）=sin（2x+φ）（0＜φ＜π）的图象向右平移2个单位后，
得到y=sin[2（x-2）+φ]=sin（2x-4+φ）的图象，
再根据得到的函数图象关于原点对称，∴-4+φ=kπ，k∈Z，
则实数φ的值为4-π，
故答案为：4-π．
点评 本题主要考查y=Asin（ωx+φ）的图象变换规律，正弦函数、余弦函数的奇偶性，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．$sin\frac{2015π}{3}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
5．若将函数f（x）=sin（2x+$\frac{π}{3}$）的图象向右平移ϕ个单位长度，可以使f（x）成为奇函数，则ϕ的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
2．为了了解高一、高二、高三的身体状况，现用分层抽样的方法抽出一个容量为1200的样本，三个年级学生数之比依次为k：5：3，已知高一年级共抽取了240人，则高三年级抽取的人数为（ ）
| A． | 240 | B． | 300 | C． | 360 | D． | 400 |
9．
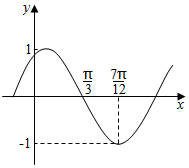函数f（x）=Asin（ωx+φ）（A＞0，|φ|＜$\frac{π}{2}$）其中的图象如图所示，为了得到g（x）=cos（2x-$\frac{π}{2}$）的图象，只需将f（x）的图象（ ）
函数f（x）=Asin（ωx+φ）（A＞0，|φ|＜$\frac{π}{2}$）其中的图象如图所示，为了得到g（x）=cos（2x-$\frac{π}{2}$）的图象，只需将f（x）的图象（ ）| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{π}{6}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
3．椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的短轴长为（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 4 | D． | 2 |
4．
如图，正四棱台ABCD-A1B1C1D1的上底面边长为1，下底面边长为3，高为1，M为BC的中点，则直线B1M与平面ACC1A1的夹角的正弦值为（ ）
如图，正四棱台ABCD-A1B1C1D1的上底面边长为1，下底面边长为3，高为1，M为BC的中点，则直线B1M与平面ACC1A1的夹角的正弦值为（ ）| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{3}}{6}$ |