题目内容
4.在平面直角坐标系中,已知点A(0,0),B(1,1),C(2,-1),则∠BAC的余弦值为$\frac{\sqrt{10}}{10}$.分析 利用两点之间的距离的距离公式、余弦定理即可得出.
解答 解:|AB|=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,|AC|=$\sqrt{5}$,|BC|=$\sqrt{5}$.
∴cos∠BAC=$\frac{|AB{|}^{2}+|AC{|}^{2}-|BC{|}^{2}}{2|AB||AC|}$=$\frac{2+5-5}{2×\sqrt{2}×\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
故答案为:$\frac{\sqrt{10}}{10}$.
点评 本题考查了两点之间的距离的距离公式、余弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
14.函数y=ln(-x2-2x+8)的单调递减区间是( )
| A. | (-∞,-1) | B. | (-1,2) | C. | (-4,-1) | D. | (-1,+∞) |
16.函数y=log3|x|的图象大致形状是( )
| A. | 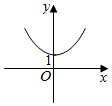 | B. |  | C. | 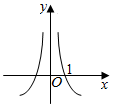 | D. | 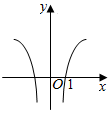 |
13.已知函数f(x)=3-ax+1的图象恒过定点P,则点P的坐标是( )
| A. | (0,3) | B. | (-1,2) | C. | (-1,3) | D. | (3,-1) |
14.设函数f(x)=$\left\{\begin{array}{l}{2x+1,x>0}\\{0,x=0}\\{2x-1,x<0}\end{array}\right.$若不等式f(x-1)+f($\frac{m}{x}$)>0对任意x>0恒成立,则实数m的取值范围是( )
| A. | ($-\frac{1}{4}$,$\frac{1}{4}$) | B. | (0,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,+∞) | D. | (1,+∞) |