题目内容
已知f(x)是二次函数,若f(0)=0,f(1)=2,且不等式f(x)≥3x-1对x∈R恒成立.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若方程f(x)=2kx-k2+3的两根为x1,x2,且满足x1+1=2x2,求实数k的值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若方程f(x)=2kx-k2+3的两根为x1,x2,且满足x1+1=2x2,求实数k的值.
考点:一元二次方程的根的分布与系数的关系,二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)设函数f(x)=ax2+bx+c,则由f(0)=0,f(1)=2,求得f(x)=ax2+(2-a)x.再根据ax2-(a+1)x+1≥0 恒成立,故有
,求得a的值,可得f(x)的解析式.
(Ⅱ)若方程f(x)=2kx-k2+3的两根为x1,x2,则由题意可得
,化简可得k2+6k-27=0,由此解得k的值.
|
(Ⅱ)若方程f(x)=2kx-k2+3的两根为x1,x2,则由题意可得
|
解答:
解:(Ⅰ)设函数f(x)=ax2+bx+c,则由f(0)=0,f(1)=2,
可得c=0,a+b=2,∴f(x)=ax2+(2-a)x.
再根据f(x)≥3x-1对x∈R恒成立,可得ax2+(2-a)x≥3x-1对x∈R恒成立,
即ax2-(a+1)x+1≥0 恒成立,故有
,a=1,
∴f(x)=x2+x.
(Ⅱ)若方程f(x)=2kx-k2+3的两根为x1,x2,即x2-(2k-1)x+k2-3=0的两根为x1,x2,
则由题意可得
,化简可得k2+6k-27=0,解得k=-9,或k=3,
都满足判别式△≥0,故k=-9,或k=3.
可得c=0,a+b=2,∴f(x)=ax2+(2-a)x.
再根据f(x)≥3x-1对x∈R恒成立,可得ax2+(2-a)x≥3x-1对x∈R恒成立,
即ax2-(a+1)x+1≥0 恒成立,故有
|
∴f(x)=x2+x.
(Ⅱ)若方程f(x)=2kx-k2+3的两根为x1,x2,即x2-(2k-1)x+k2-3=0的两根为x1,x2,
则由题意可得
|
都满足判别式△≥0,故k=-9,或k=3.
点评:本题主要考查了一元二次方程的根的分布与系数的关系,二次函数的性质,属于基础题.

练习册系列答案
相关题目
函数y=ax2+bx+c与y=ax+b(ab≠0)的图象可能是( )
A、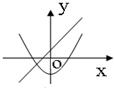 |
B、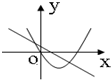 |
C、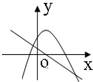 |
D、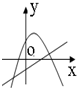 |