题目内容
16．已知命题p：?x＜1，$log{\;}_{\frac{1}{3}}x＜0$；命题q：?x0∈R，$x_0^2≥{2^{x_0}}$，则下列命题中为真命题的是（ ）| A． | p∨q | B． | （￢p）∧（￢q） | C． | p∨（￢q） | D． | p∧q |
分析 命题p：是假命题，例如x≤0时无意义；命题q：是真命题，例如取x0=2时成立．再利用复合命题真假的判定方法即可判断出结论．
解答 解：命题p：?x＜1，$log{\;}_{\frac{1}{3}}x＜0$，是假命题，例如x≤0时无意义；
命题q：?x0∈R，$x_0^2≥{2^{x_0}}$，是真命题，例如取x0=2时成立．
则下列命题中为真命题的是p∨q．
故选：A．
点评 本题考查了函数的单调性、复合命题真假的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
18．已知某产品的广告费用x（单位：万元）与销售额y（单位：万元）具有线性关系关系，其统计数据如下表：
由上表可得线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，据此模型预报广告费用为8万元时的销售额是（ ）
附：$\widehat{b}$=$\frac{{\sum_{i=1}^n{（{x_i}-\overline x）•（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}$；$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x．
| x | 3 | 4 | 5 | 6 |
| y | 25 | 30 | 40 | 45 |
附：$\widehat{b}$=$\frac{{\sum_{i=1}^n{（{x_i}-\overline x）•（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}$；$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x．
| A． | 59.5 | B． | 52.5 | C． | 56 | D． | 63.5 |
19．已知集合A={x∈R|0＜x≤5}，B={x∈R|log2x＜2}，则（∁AB）∩Z=（ ）
| A． | {4} | B． | {5} | C． | [4，5] | D． | {4，5} |
11．函数y=（x+1）3当x=-1时（ ）
| A． | 有极大值 | B． | 有极小值 | ||
| C． | 既无极大值，也无极小值 | D． | 无法判断 |
1．
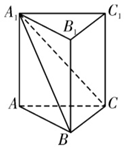在我国古代数学名著《九章算术》中将底面为直角三角形，且侧棱垂直于底面的三棱柱称之为堑堵，如图，在堑堵ABC-A1B1C1中，AB=BC，AA1＞AB，堑堵的顶点C1到直线A1C的距离为m，C1到平面A1BC的距离为n，则$\frac{m}{n}$的取值范围是（ ）
在我国古代数学名著《九章算术》中将底面为直角三角形，且侧棱垂直于底面的三棱柱称之为堑堵，如图，在堑堵ABC-A1B1C1中，AB=BC，AA1＞AB，堑堵的顶点C1到直线A1C的距离为m，C1到平面A1BC的距离为n，则$\frac{m}{n}$的取值范围是（ ）| A． | （1，$\frac{2\sqrt{3}}{3}$） | B． | （$\frac{\sqrt{2}}{2}$，$\frac{2\sqrt{3}}{3}$） | C． | （$\frac{2\sqrt{3}}{3}$，$\sqrt{3}$） | D． | （$\frac{2\sqrt{3}}{3}$，$\sqrt{2}$） |