题目内容
1.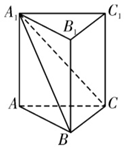 在我国古代数学名著《九章算术》中将底面为直角三角形,且侧棱垂直于底面的三棱柱称之为堑堵,如图,在堑堵ABC-A1B1C1中,AB=BC,AA1>AB,堑堵的顶点C1到直线A1C的距离为m,C1到平面A1BC的距离为n,则$\frac{m}{n}$的取值范围是( )
在我国古代数学名著《九章算术》中将底面为直角三角形,且侧棱垂直于底面的三棱柱称之为堑堵,如图,在堑堵ABC-A1B1C1中,AB=BC,AA1>AB,堑堵的顶点C1到直线A1C的距离为m,C1到平面A1BC的距离为n,则$\frac{m}{n}$的取值范围是( )| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{3}}{3}$) | C. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
分析 设AB=1,AA1=a,用a表示出m,n,得出$\frac{m}{n}$关于a的函数,根据a的范围可求出$\frac{m}{n}$的范围.
解答 解:设AB=BC=1,则AC=A1C1=$\sqrt{2}$,设AA1=a,则CC1=a,
∴A1C=$\sqrt{{a}^{2}+2}$,
∴C1到直线A1C的距离m=$\frac{{A}_{1}{C}_{1}•C{C}_{1}}{{A}_{1}C}$=$\frac{\sqrt{2}a}{\sqrt{{a}^{2}+2}}$,
∵B1C1∥BC,BC?平面A1BC,B1C1?平面A1BC,
∴B1C1∥平面A1BC,
∴C1到平面A1BC的距离等于B1到平面A1BC的距离,
∴V${\;}_{{B}_{1}-{A}_{1}BC}$=$\frac{1}{3}{S}_{△{A}_{1}BC}•n$,
∵BC⊥AB,BC⊥BB1,AB∩BB1=B,
∴BC⊥平面ABB1A1,
∴BC⊥A1B,∴S${\;}_{△{A}_{1}BC}$=$\frac{1}{2}•BC•{A}_{1}B$=$\frac{1}{2}×1×\sqrt{{a}^{2}+1}$=$\frac{\sqrt{{a}^{2}+1}}{2}$,
又VV${\;}_{{B}_{1}-{A}_{1}BC}$=V${\;}_{C-AB{B}_{1}}$=$\frac{1}{3}{S}_{△AB{B}_{1}}•BC$=$\frac{1}{3}×\frac{1}{2}×1×a×1$=$\frac{a}{6}$,
∴$\frac{1}{3}$•$\frac{\sqrt{{a}^{2}+1}}{2}$•n=$\frac{a}{6}$,∴n=$\frac{a}{\sqrt{{a}^{2}+1}}$.
∴$\frac{m}{n}$=$\frac{\sqrt{2}•\sqrt{{a}^{2}+1}}{\sqrt{{a}^{2}+2}}$=$\sqrt{\frac{2{a}^{2}+2}{{a}^{2}+2}}$=$\sqrt{2-\frac{2}{{a}^{2}+2}}$.
∵AA1>AB,∴a>1,
∴0<$\frac{2}{{a}^{2}+2}$<$\frac{2}{3}$,
∴$\frac{2\sqrt{3}}{3}$<$\sqrt{2-\frac{2}{{a}^{2}+2}}$$<\sqrt{2}$.
故选D.
点评 本题考查了棱柱的结构特征,空间距离的计算,属于中档题.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案| A. | p∨q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧q |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 总计 | |
| 物理成绩优秀 | 5 | 2 | 7 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 总计 | 6 | 14 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
(2)据此估计广告费用为12时,销售收入y的值.
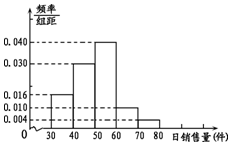 某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.
某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.