题目内容
5.已知f($\frac{1}{{2}^{n+1}}$)=$\frac{1}{2}$f($\frac{1}{{2}^{n}}$)-$\frac{1}{{2}^{n+1}}$,f($\frac{1}{2}$)=-$\frac{1}{2}$,令Un=$\frac{f(\frac{1}{{2}^{n}})}{n}$,则{Un}的前n项和Tn=$\frac{1}{{2}^{n}}$-1.分析 f($\frac{1}{{2}^{n}}$)=$\frac{1}{2}$f($\frac{1}{{2}^{n-1}}$)-$\frac{1}{{2}^{n}}$=…=($\frac{1}{2}$)n-1f($\frac{1}{2}$)-$\frac{n-1}{{2}^{n}}$=-$\frac{n}{{2}^{n}}$,再根据等比数列的求和公式计算即可.
解答 解:∵f($\frac{1}{{2}^{n+1}}$)=$\frac{1}{2}$f($\frac{1}{{2}^{n}}$)-$\frac{1}{{2}^{n+1}}$,
∴f($\frac{1}{{2}^{n}}$)=$\frac{1}{2}$f($\frac{1}{{2}^{n-1}}$)-$\frac{1}{{2}^{n}}$=($\frac{1}{2}$)2f($\frac{1}{{2}^{n-2}}$)-$\frac{2}{{2}^{n}}$=($\frac{1}{2}$)3f($\frac{1}{{2}^{n-3}}$)-$\frac{3}{{2}^{n}}$=…=($\frac{1}{2}$)n-1f($\frac{1}{2}$)-$\frac{n-1}{{2}^{n}}$=-($\frac{1}{2}$)n-$\frac{n-1}{{2}^{n}}$=-$\frac{n}{{2}^{n}}$,
∴Un=$\frac{f(\frac{1}{{2}^{n}})}{n}$=-$\frac{1}{{2}^{n}}$,
∴{Un}的前n项和Tn=-$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=$\frac{1}{{2}^{n}}$-1,
故答案为:$\frac{1}{{2}^{n}}$-1
点评 本题考查了数列的函数特征,由函数关系式可得数列的通项公式是关键,属于中档题.

| A. | p∨q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧q |
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
(2)据此估计广告费用为12时,销售收入y的值.
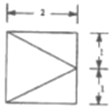 己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )
己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )| A. | 8π | B. | 12π | C. | 4π | D. | 16π |
| A. | $\frac{2}{e}f(2)<f(1)$ | B. | $\frac{2}{e}f(2)>f(1)$ | C. | f(1)>0 | D. | f(-1)>0 |