题目内容
6.设p:实数x满足x2-4ax+3a2<0(其中a>0),q:2<x≤3.若p是q的必要不充分条件,则实数a的取值范围是(1,2].分析 p:实数x满足x2-4ax+3a2<0(其中a>0),解得a<x<3a.根据p是q的必要不充分条件,可得$\left\{\begin{array}{l}{a≤2}\\{3<3a}\end{array}\right.$,解出即可得出.
解答 解:p:实数x满足x2-4ax+3a2<0(其中a>0),解得a<x<3a.
q:2<x≤3.
∵p是q的必要不充分条件,∴$\left\{\begin{array}{l}{a≤2}\\{3<3a}\end{array}\right.$,
解得1<a≤2.
则实数a的取值范围是(1,2],
故答案为:(1,2].
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
7.定义在R上的偶函数f(x)满足f(2+x)=f(x),且在[-3,-2]上是减函数,若A、B是锐角三角形ABC的两个内角,则下列各式一定成立的是( )
| A. | f(sinA)<f(cosB) | B. | f(sinA)>f(cosB) | C. | f(sinA)>f(sinB) | D. | f(cosA)>f(cosB) |
14.过点P(2,-3)的等轴双曲线的标准方程为( )
| A. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{13}$-$\frac{{y}^{2}}{13}$=1 | C. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{13}$-$\frac{{x}^{2}}{13}$=1 |
18.直线l:$\frac{x}{m}$+$\frac{y}{n}$=1过点A(1,2),则直线l与x、y正半轴围成的三角形的面积的最小值为( )
| A. | 2$\sqrt{2}$ | B. | 3 | C. | $\frac{5\sqrt{2}}{2}$ | D. | 4 |
15.过点P(-4,0)作函数y=$\sqrt{4-{x}^{2}}$的切线l,则切线l的方程为( )
| A. | y=$\sqrt{3}$(x+4) | B. | y=$\frac{\sqrt{3}}{3}$(x+4) | C. | y=$\frac{\sqrt{2}}{2}$(x+4) | D. | y=$\sqrt{2}$(x+4) |
16.给出程序框图如图所示,若输入n=20,则输出S=( )
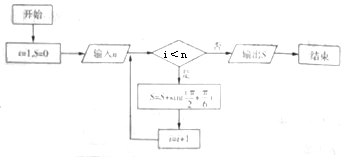

| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{\sqrt{3}}{2}$ |
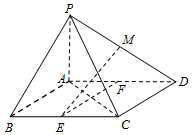 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=45°,PA⊥底面ABCD,AB=AC=PA=2,E、F分别为BC、AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=45°,PA⊥底面ABCD,AB=AC=PA=2,E、F分别为BC、AD的中点,点M在线段PD上.