题目内容
1.给出以下命题:①若cos<$\overrightarrow{MN}$,$\overrightarrow{PQ}$>=-$\frac{1}{3}$,则异面直线MN与PQ所成角的余弦值为-$\frac{1}{3}$;
②若平面α与β的法向量分别是$\overrightarrow a=(2,4,-3)$与$\overrightarrow b=(-1,2,2)$,则平面α⊥β;
③已知A、B、C三点不共线,点O为平面ABC外任意一点,若点M满足$\overrightarrow{OM}=\frac{1}{5}\overrightarrow{OA}+\frac{4}{5}\overrightarrow{OB}+\frac{2}{5}\overrightarrow{BC}$,则点M∈平面ABC;
④若向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$是空间的一个基底,则向量$\overrightarrow a+\overrightarrow b+\overrightarrow c$、$\overrightarrow a+\overrightarrow b$、$\overrightarrow c$也是空间的一个基底;
则其中正确的命题个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由两条异面直线所成的角的取值范围可以判断①,由平面向量数量积的运算可以判断②,在空间,点M在平面ABC内的充要条件是存在α、β、γ,使$\overrightarrow{OM}$=α$\overrightarrow{OA}$+β $\overrightarrow{OB}$+γ$\overrightarrow{OC}$且α+β+γ=1可以判断③,由三个向量非零不共线可以判断④,从而可得到正确的命题个数.
解答 解:对于①:∵两条异面直线所成的角的取值范围是(0°,90°],
∴异面直线MN与PQ所成角的余弦值不能为负值,故①不正确;
对于②:∵$\overrightarrow{a}$•$\overrightarrow{b}$=(2,4,-3)(-1,2,2)=-2+8-6=0,
∴$\overrightarrow{a}$⊥$\overrightarrow{b}$.∴平面α与平面β垂直,故②正确;
对于③:∵$\overrightarrow{OM}=\frac{1}{5}\overrightarrow{OA}+\frac{4}{5}\overrightarrow{OB}+\frac{2}{5}\overrightarrow{BC}$,且$\frac{1}{5}+\frac{4}{5}+\frac{2}{5}=\frac{7}{5}≠1$
∴M点不在平面ABC内,故③不正确;
对于④:∵向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow c$是空间的一个基底,则向量$\overrightarrow a+\overrightarrow b+\overrightarrow c$、$\overrightarrow a+\overrightarrow b$、$\overrightarrow c$也是空间的一个基底,∵三个向量非零不共线,故④正确.
∴其中正确的命题个数是:2.
故选:B.
点评 本题考查了命题的真假判断与应用,考查了两条异面直线所成的角的取值范围以及平面向量数量积的运算,是中档题.

| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
| A. | (-2,-1) | B. | (2,5) | C. | (-2,-1] | D. | (-∞,2)∪[5,+∞) |
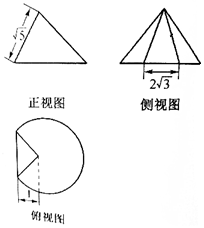 一个圆锥被过顶点的平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )
一个圆锥被过顶点的平面截去了较少的一部分几何体,余下的几何体的三视图如图,则余下部分的几何体的体积为( )| A. | $\frac{8π}{3}$+$\sqrt{15}$ | B. | $\frac{16π}{3}$+$\sqrt{3}$ | C. | $\frac{8π}{3}$+$\frac{2\sqrt{3}}{3}$ | D. | $\frac{16π}{9}$+$\frac{2\sqrt{3}}{3}$ |
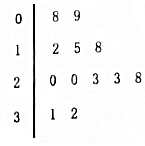 广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )
广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )| A. | 20;23 | B. | 21.5;20,23 | C. | 20;20,23 | D. | 21.5;23 |
| A. | 1023 | B. | 55 | C. | 45 | D. | 35 |
| A. | $ω=2,ϕ=\frac{π}{3}$ | B. | $ω=2,ϕ=\frac{π}{6}$ | C. | $ω=4,ϕ=\frac{π}{6}$ | D. | $ω=2,ϕ=-\frac{π}{6}$ |