题目内容

cos
π
3
-tan
π
4
+
3
4
tan2
π
6
-sin
π
6
+cos2
π
6
．
考点：三角函数的化简求值
专题：三角函数的求值
分析：直接利用特殊角的三角函数化简求解即可．
解答： 解：cos
π
3
-tan
π
4
+
3
4
tan2
π
6
-sin
π
6
+cos2
π
6

=
1
2
-1+
3
4
×(
3
3
)2-
1
2
+(
3
2
)2
=0．
点评：本题考查三角函数化简求值，特殊角的三角函数值的求法，考查计算能力．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，PA=PD=AD=2．
（1）求证：AD⊥平面PQB；
（2）若PM=
1
3
PC，平面PAD⊥平面ABCD，求二面角M-BQ-C的大小．
如图所示，在等腰直角三角形ABC中，AC=AB=2
2
，E为AB的中点，点F在BC 上，且EF⊥BC．现沿EF 将△BEF 折1起到△PEF的位置，使PF⊥CF，点D 在PC上，且PD=
1
2
DC．
（1）求证：AD∥平面PEF；
（2）求二面角A-PC-F的余弦值．
设非零向量向量
OA
=
a
，
OB
=
b
，已知|
a
|=2|
b
|，（
a
+
b
）⊥
b
．
（1）求
a
与
b
的夹角；
（2）在如图所示的直角坐标系xOy中，设B（1，0），已知
M（
1
2
，
5
3
6
），
OM
=λ1
a
+λ2
b
（λ1，λ2∈R），求λ1+λ2的值．
已知函数f（x）=
x+2
+k，k为已知的实数．
（1）求函数f（x）的值域；并判断其在定义域上的单调性（不必证明）；
（2）当k=-2时，设f（x）≤0的解集为A，函数g（x）=lg（sin2
π
6
x-3sin
π
6
xcos
π
6
x+acos2
π
6
x）的定义域为B，若（A∪B）⊆B，求实数a的取值范围；
（3）若存在实数-2≤a＜b，使f（x）在[a，b]上的值域为[2a，2b]，求实数k的取值范围．
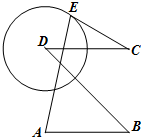如图所示，正方形ABCD边长为2，圆D的半径为1，E是圆D上任意一点，则
AE
•
CE
的最小值为（　　）
A、1+2
2
B、-1-2
2
C、1-
2
D、1-2
2
∫
π
2
-π
（xcosx+sinx）dx=
 
．
已知：如图，在Rt△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过点D作DE⊥BC，垂足为E，连接EA交⊙O于点F．求证：
（Ⅰ）DE是⊙O的切线；
（Ⅱ）BE•CE=EF•EA．
已知正项数列{an}的前n项和Sn，且2
Sn
=an十1，n∈N*
（1）试求数列{an}的通项公式，
（2）设bn=
1
anan+1
，数列{bn}的前n项和为Bn，求证：Bn＜
1
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网