题目内容
已知向量
=（cos
，sin
），
=（cos
，-sin
），x∈[0，
]
（Ⅰ）用含x的式子表示
•
及|
+
|；
（Ⅱ）求函数f（x）=|
+
|的值域；
（Ⅲ）设g（x）=
•
+t|
+
|，若关于x的方程g（x）+2=0有两个不同的实数解，求实数t的取值范围．
| a |
| 3x |
| 2 |
| 3x |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
（Ⅰ）用含x的式子表示
| a |
| b |
| a |
| b |
（Ⅱ）求函数f（x）=|
| a |
| b |
（Ⅲ）设g（x）=
| a |
| b |
| a |
| b |
考点：平面向量的综合题
专题：平面向量及应用
分析：（Ⅰ）由已知得
•
=cos
cos
-sin
sin
=cos2x，由此能求出
•
及|
+
|．
（Ⅱ）f（x）=
•
-4|
+
|=2（cosx-2）2-9，由此能求出f（x）的值域．
（Ⅲ）由g（x）+2=0，得：2cos2x+2tcosx+1=0，令cosx=u∈[0，1]，F（μ）=2μ2+2tμ+1，由此能求出实数t的取值范围．
| a |
| b |
| 3x |
| 2 |
| x |
| 2 |
| 3x |
| 2 |
| x |
| 2 |
| a |
| b |
| a |
| b |
（Ⅱ）f（x）=
| a |
| b |
| a |
| b |
（Ⅲ）由g（x）+2=0，得：2cos2x+2tcosx+1=0，令cosx=u∈[0，1]，F（μ）=2μ2+2tμ+1，由此能求出实数t的取值范围．
解答：
解：（Ⅰ）∵
=（cos
，sin
），
=（cos
，-sin
），x∈[0，
]，
∴
•
=cos
cos
-sin
sin
=cos2x，…（2分）
|
+
|2=1+2cos2x+1
=2（1+cos2x）
=4cos2x，
∴|
+
|=2cosx，x∈[0，
]．…（4分）
（Ⅱ）f（x）=
•
-4|
+
|=cos2x-8cosx=2cos2x-8cosx-1=2（cosx-2）2-9，
又x∈[0，
]，
∴cosx∈[0，1]，f（x）∈[-7，-1]．…（8分）
（Ⅲ）由g（x）+2=0，
得：2cos2x+2tcosx+1=0，
令cosx=u∈[0，1]，F（μ）=2μ2+2tμ+1，
∴
，…（10分）
解得t∈[-
，-
）．…（12分）
| a |
| 3x |
| 2 |
| 3x |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
∴
| a |
| b |
| 3x |
| 2 |
| x |
| 2 |
| 3x |
| 2 |
| x |
| 2 |
|
| a |
| b |
=2（1+cos2x）
=4cos2x，
∴|
| a |
| b |
| π |
| 2 |
（Ⅱ）f（x）=
| a |
| b |
| a |
| b |
又x∈[0，
| π |
| 2 |
∴cosx∈[0，1]，f（x）∈[-7，-1]．…（8分）
（Ⅲ）由g（x）+2=0，
得：2cos2x+2tcosx+1=0，
令cosx=u∈[0，1]，F（μ）=2μ2+2tμ+1，
∴
|
解得t∈[-
| 3 |
| 2 |
| 2 |
点评：本题考查向量的数量积和向量的模的求法，考查函数的值域的求法，考查实数的取值范围的求法，解题时要认真审题，注意平面向量知识的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
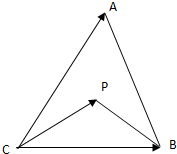如图示，已知A、B、C为平面上的三个定点，∠ACB=60°，动点P在∠ACB的平分线上，记