题目内容
设F1、F2分别是椭圆
+
=1(a>b>0)的左、右焦点,P为椭圆上的任意一点,满足|PF1|+|PF2|=8,△PF1F2的周长为12.
(1)求椭圆的方程;
(2)求
•
的最大值和最小值.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的方程;
(2)求
| PF1 |
| PF2 |
考点:椭圆的标准方程,平面向量数量积的运算
专题:圆锥曲线的定义、性质与方程
分析:(1)由已知得2a=8,2a+2c=12,由此能求出椭圆方程.
(2)设P(x,y),则
•
=(-2-x,-y)•(2-x,-y)=
x2+8,由此能求出
•
的最大值和最小值.
(2)设P(x,y),则
| PF1 |
| PF2 |
| 1 |
| 4 |
| PF1 |
| PF2 |
解答:
解:(1)由已知得2a=8,2a+2c=12,
解得a=4,c=2,
∴b2=16-4=12,
∴椭圆方程为
+
=1.
(2)∵椭圆方程为
+
=1,
∴F1(-2,0),F2(2,0),
设P(x,y),
则
•
=(-2-x,-y)•(2-x,-y)
=x2+y2-4
=x2+12-
x2-4
=
x2+8,
∵x∈[-4,4],∴x2∈[0,16],
∴8≤
•
≤12,
点P为椭圆短轴端点时,
•
有最小值8,
点P为椭圆长轴端点时,
•
有最大值12.
解得a=4,c=2,
∴b2=16-4=12,
∴椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)∵椭圆方程为
| x2 |
| 16 |
| y2 |
| 12 |
∴F1(-2,0),F2(2,0),
设P(x,y),
则
| PF1 |
| PF2 |
=x2+y2-4
=x2+12-
| 3 |
| 4 |
=
| 1 |
| 4 |
∵x∈[-4,4],∴x2∈[0,16],
∴8≤
| PF1 |
| PF2 |
点P为椭圆短轴端点时,
| PF1 |
| PF2 |
点P为椭圆长轴端点时,
| PF1 |
| PF2 |
点评:本题考查椭圆方程的求法,考查
•
的最大值和最小值的求法,解题时要认真审题,注意椭圆性质的合理运用.
| PF1 |
| PF2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
从只含有二件次品的10个产品中取出三件,设A为“三件产品不全是次品”,B为“三件产品全不是次品”,C为“三件产品全是次品”,则下列结论正确的是( )
| A、事件A与B互斥 |
| B、事件A是随机事件 |
| C、任两个均互斥 |
| D、事件C是不可能事件 |
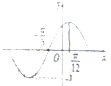 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0),|φ|≤| π |
| 2 |
A、f(x)=sin(2x+
| ||
B、f(x)=sin(2x-
| ||
C、f(x)=sin(4x+
| ||
D、f(x)=sin(4x-
|
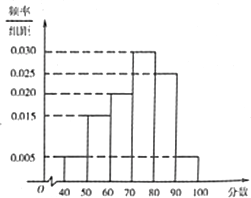 育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为
育才中学从参加高二年级学业水平测试的学生中抽出100名学生,其数学成绩的频率分布直方图如下图所示.其中成绩分组区间是[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].则成绩在[80,100]上的人数为