题目内容
12．已知点P是边长为4的正方形内任一点，则点P到四个顶点的距离均大于2的概率是1$-\frac{π}{4}$．分析 根据题意，先求出满足条件的正方形ABCD的面积，再求出满足条件正方形内的点到正方形的顶点A、B、C、D的距离均不小于2的图形的面积，然后代入几何概型公式即可得到答案．
解答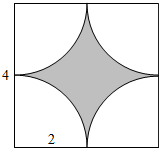 
解：满足条件的正方形ABCD如下图所示：
其中正方形的面积S正方形=4×4=16；
满足到正方形的顶点A、B、C、D的距离均不小于2的平面区域如图中阴影部分所示
则S阴影=16-4π，
故该正方形内的点到正方形的顶点A、B、C、D的距离均不小于1的概率是P=$\frac{{S}_{阴影}}{{S}_{正方形}}$=$\frac{16-4π}{16}$=1$-\frac{π}{4}$；
故答案为：1$-\frac{π}{4}$．
点评 本题考查几何概型的计算，解题的关键理解几何概型的意义，即将长度、面积、体积的比值转化为事件发生的概率
练习册系列答案
相关题目
2．若双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的其渐近线方程为（ ）
| A． | y=±2x | B． | $y=±\frac{{\sqrt{2}}}{2}x$ | C． | $y=±\frac{1}{2}x$ | D． | $y=±\sqrt{2}x$ |
20．已知平面向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$满足$\overrightarrow c=x\overrightarrow a+y\overrightarrow b$（x，y∈R），且$\overrightarrow a•\overrightarrow c＞0$，$\overrightarrow b•\overrightarrow c＞0$．（ ）
| A． | 若$\overrightarrow a•\overrightarrow b＜0$，则x＞0，y＞0 | B． | 若$\overrightarrow a•\overrightarrow b＜0$，则x＜0，y＜0 | ||
| C． | 若$\overrightarrow a•\overrightarrow b＞0$，则x＜0，y＜0 | D． | 若$\overrightarrow a•\overrightarrow b＞0$，则x＞0，y＞0 |
7．函数f（x）=$\frac{1}{x^2-x}$+$\sqrt{2-x}$的定义域是（ ）
| A． | （-∞，1）∪（1，2） | B． | （-∞，0）∪（0，1）∪（1，2） | C． | （-∞，0）∪（1，2） | D． | （-∞，0）∪（0，1）∪（1，2] |
4．若实数x，y满足不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≤1\\ x≥0\end{array}\right.$，则2x+y的最大值是（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
1．已知函数f（x）是R上的增函数，A（0，-3），B（3，1）是其图象上的两点，那么不等式-3＜f（x+1）＜1的解集的补集是（ ）
| A． | （-1，2） | B． | （1，4） | C． | （-∞，-1）∪[4，+∞） | D． | （-∞，-1]∪[2，+∞） |