题目内容
2．已知x，y∈{1，2，3，4，5，6}，且x+y=7，则$y≥\frac{x}{2}$的概率（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{6}$ |
分析 先列举出所有的基本事件，再找到满足条件的基本事件，根据概率公式计算即可．
解答 解：由题基本事件空间中的元素有：（1，6），（2，5），（3，4），（4，3），（5，2）（6，1），
满足题意的有（1，6），（2，5），（3，4），（4，3），
故则$y≥\frac{x}{2}$的概率为$\frac{4}{6}$=$\frac{2}{3}$
故选：B．
点评 本题考查了古典概率的问题，关键是一一列举，属于基础题．
练习册系列答案
相关题目
13．
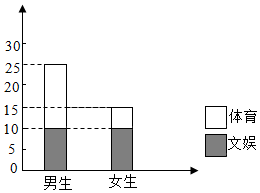对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（1）根据图中数据，制作2×2列联表；
（2）若要采用分层抽样的方法从男生中共抽取5名候选人，再从5人中选两人分别做文体活动协调人，求选出的两人恰好是一人更爱好文娱，另一人更爱好体育的学生的概率；
（3）是否可以认为性别与是否爱好体育有关系？
参考数据：
对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．（1）根据图中数据，制作2×2列联表；
（2）若要采用分层抽样的方法从男生中共抽取5名候选人，再从5人中选两人分别做文体活动协调人，求选出的两人恰好是一人更爱好文娱，另一人更爱好体育的学生的概率；
（3）是否可以认为性别与是否爱好体育有关系？
参考数据：
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
△ABC中，AB=1，AC=2．
7．已知函数$f（x）=\left\{{\begin{array}{l}{x+\frac{1}{2}，x∈[0，\frac{1}{2}）}\\{{2^{x-1}}，x∈[\frac{1}{2}，2）}\end{array}}\right.$，若存在x1，x2，当0≤x1＜x2＜2时，f（x1）=f（x2），则x1f（x2）-f（x2）的取值范围为（ ）
| A． | $（0，\frac{{2-3\sqrt{2}}}{4}）$ | B． | $[-\frac{9}{16}，\frac{{2-3\sqrt{2}}}{4}）$ | C． | $[\frac{{2-3\sqrt{2}}}{4}，-\frac{1}{2}）$ | D． | $[-\frac{9}{16}，-\frac{1}{2}）$ |
11．已知集合A={3，$\sqrt{a}$}，B={a，b}，若A∩B={2}，则A∪B=（ ）
| A． | {2，3} | B． | {3，4} | C． | {$\sqrt{2}$，2，3} | D． | {2，3，4} |