题目内容
19.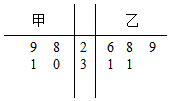 为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲、乙两地某月11时的气温情况,随机选取该月中的5天中11时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月11时的平均气温低于乙地该月11时的平均气温
②甲地该月11时的平均气温高于乙地该月11时的平均气温
③甲地该月11时的气温的标准差小于乙地该月11时的气温的标准差
④甲地该月11时的气温的标准差大于乙地该月11时的气温的标准差
其中根据茎叶图能得到的正确结论的编号为( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
分析 根据茎叶图中的数据,分别求出甲、乙两地某月11时气温这两组数据的平均数、方差即可.
解答 解:由茎叶图中的数据知,乙两地某月11时的气温分别为:
甲:28,29,30,31,32
乙:26,28,29,31,31;
可得:甲地该月11时的平均气温为$\overline{{x}_{甲}}$=$\frac{1}{5}$(28+29+30+31+32)=30,
乙地该月11时的平均气温为$\overline{{x}_{乙}}$=$\frac{1}{5}$(26+28+29+31+31)=29,
故甲地该月11时的平均气温高于乙地该月11时的平均气温;①错误,②正确;
又甲地该月11时温度的方差为${{s}_{甲}}^{2}$=$\frac{1}{5}$[(28-30)2+(29-30)2+(30-30)2+(31-30)2+(32-30)2]=2
乙地该月14时温度的方差为${{s}_{乙}}^{2}$=$\frac{1}{5}$[(26-29)2+(28-29)2+(29-29)2+(31-29)2+(31-29)2]=3.6,
故${{s}_{甲}}^{2}$<${{s}_{乙}}^{2}$,
所以甲地该月11时的气温标准差小于乙地该月11时的气温标准差,③正确,④错误.
综上,正确的命题是②③.
故选:C.
点评 本题考查了数据的平均数与方差的计算问题,也考查了计算能力的应用问题,是基础题目.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
7.已知函数$f(x)=\left\{{\begin{array}{l}{x+\frac{1}{2},x∈[0,\frac{1}{2})}\\{{2^{x-1}},x∈[\frac{1}{2},2)}\end{array}}\right.$,若存在x1,x2,当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)-f(x2)的取值范围为( )
| A. | $(0,\frac{{2-3\sqrt{2}}}{4})$ | B. | $[-\frac{9}{16},\frac{{2-3\sqrt{2}}}{4})$ | C. | $[\frac{{2-3\sqrt{2}}}{4},-\frac{1}{2})$ | D. | $[-\frac{9}{16},-\frac{1}{2})$ |
4.设集合M={x|$\frac{1}{2}≤x<3$},函数f(x)=ln(1-$\sqrt{x}$)的定义域为N,则M∩N为( )
| A. | [$\frac{1}{2}$,1] | B. | [$\frac{1}{2}$,1) | C. | (0,$\frac{1}{2}$] | D. | (0,$\frac{1}{2}$) |
11.已知集合A={3,$\sqrt{a}$},B={a,b},若A∩B={2},则A∪B=( )
| A. | {2,3} | B. | {3,4} | C. | {$\sqrt{2}$,2,3} | D. | {2,3,4} |
8.已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意的实数x都有f(x)≥0,则$\frac{f(1)}{{{f^'}(0)}}$的取值范围是( )
| A. | $[\frac{3}{2},+∞)$ | B. | [2,+∞) | C. | $[\frac{5}{2},+∞)$ | D. | [3,+∞) |
9.使得函数y=3-cosx取得最大值的x的集合是( )
| A. | {x|x=2kπ,k∈Z} | B. | {x|x=π+2kπ,k∈Z} | C. | {x|x=-$\frac{π}{2}$+2kπ,k∈Z} | D. | {x|x=$\frac{π}{2}$+2kπx,k∈Z} |
 △ABC中,AB=1,AC=2.
△ABC中,AB=1,AC=2.