题目内容
4．当函数f（x）=x+$\frac{1}{x-1}$，（x＞1）取得最小值时，相应的自变量x等于（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 函数f（x）=（x-1）+$\frac{1}{x-1}$+1，且x-1＞0，运用基本不等式可得f（x）的最小值3，由等号成立的条件，可得x=2．
解答 解：函数f（x）=x+$\frac{1}{x-1}$，（x＞1），
可得f（x）=（x-1）+$\frac{1}{x-1}$+1≥2$\sqrt{（x-1）•\frac{1}{x-1}}$+1=3，
当且仅当x-1=$\frac{1}{x-1}$，即x=2时，取得最小值3．
故选：A．
点评 本题考查函数的最值的求法，注意运用基本不等式，以及满足的条件：一正二定三等，考查运算能力，属于基础题．
练习册系列答案
优加精卷系列答案
相关题目
2．全集U={（x，y）|x∈R，y∈R}，集合S⊆U，若S中的点在直角坐标平面内形成的图形关于原点、坐标轴、直线y=x均对称，且（2，3）∈S，则S中元素个数至少有（ ）
| A． | 4个 | B． | 6个 | C． | 8个 | D． | 10个 |
7．在△ABC中，A，B，C的对边a，b，c满足sinC=3sinA，b2-a2=2ac，则B=（ ）
| A． | 60° | B． | 30° | C． | 120° | D． | 150° |
13．
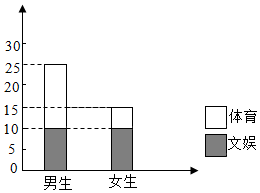对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
（1）根据图中数据，制作2×2列联表；
（2）若要采用分层抽样的方法从男生中共抽取5名候选人，再从5人中选两人分别做文体活动协调人，求选出的两人恰好是一人更爱好文娱，另一人更爱好体育的学生的概率；
（3）是否可以认为性别与是否爱好体育有关系？
参考数据：
对某班学生是爱好体育还是爱好文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．（1）根据图中数据，制作2×2列联表；
（2）若要采用分层抽样的方法从男生中共抽取5名候选人，再从5人中选两人分别做文体活动协调人，求选出的两人恰好是一人更爱好文娱，另一人更爱好体育的学生的概率；
（3）是否可以认为性别与是否爱好体育有关系？
参考数据：
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |