题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,且cos2C=cosC.
(1)求角C;
(2)若b=2a,△ABC的面积S=
sinA•sinB,求sinA及边c的值.
(1)求角C;
(2)若b=2a,△ABC的面积S=
| ||
| 2 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)已知等式左边利用二倍角的余弦函数公式化简,整理后求出cosC的值,即可确定出C的度数;
(2)利用余弦定理列出关系式,将表示出的b及cosC代入表示出c=
a,利用正弦定理化简求出sinA的值,利用三角形面积公式列出关系式,将已知面积代入求出
的值,再利用正弦定理即可求出c的值.
(2)利用余弦定理列出关系式,将表示出的b及cosC代入表示出c=
| 7 |
| ab |
| sinAsinB |
解答:
解:(1)∵cos2C=cosC,
∴2cos2C-cosC-1=0,即(2cosC+1)(cosC-1)=0,
又0<C<π,∴cosC=-
,
∴C=
;
(2)∵b=2a,cosC=-
,
∴由余弦定理得:c2=a2+(2a)2-2a•(2a)cos
=7a2,
∴c=
a,
又由正弦定理得:sinC=
sinA,
∴sinA=
;
∵S=
absinC,
∴
absinC=
sinA•sinB,即
=
=
=2,
∴由正弦定理
=
=
得:(
)2=
•
=
=2,即
=
,
解得:c=
sin
=
.
∴2cos2C-cosC-1=0,即(2cosC+1)(cosC-1)=0,
又0<C<π,∴cosC=-
| 1 |
| 2 |
∴C=
| 2π |
| 3 |
(2)∵b=2a,cosC=-
| 1 |
| 2 |
∴由余弦定理得:c2=a2+(2a)2-2a•(2a)cos
| 2π |
| 3 |
∴c=
| 7 |
又由正弦定理得:sinC=
| 7 |
∴sinA=
| ||
| 14 |
∵S=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
| ab |
| sinAsinB |
| ||
| sinC |
| ||||
|
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| c |
| sinC |
| a |
| sinA |
| b |
| sinB |
| ab |
| sinAsinB |
| c |
| sinC |
| 2 |
解得:c=
| 2 |
| 2π |
| 3 |
| ||
| 2 |
点评:此题考查了正弦、余弦定理,三角形的面积公式,二倍角的余弦函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
已知函数f(x)=aln(x+1)-x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式
>1恒成立,则实数a的取值范围为( )
| f(p+1)-f(q+1) |
| p-q |
| A、[15,+∞) |
| B、(-∞,15] |
| C、(12,30] |
| D、(-12,15] |
两条直线ax+y+1=0与3x-2y+1=0垂直,则a的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如图所示的程序框图,该算法的功能是( )
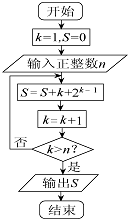

| A、计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值 |
| B、计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值 |
| C、计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值 |
| D、计算[1+2+3+…+(n-1)]+(20+21+22+…+2n)的值 |
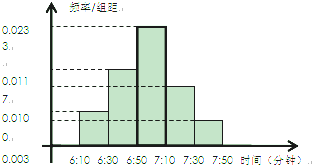 小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.