题目内容
已知不等式(m-1)x2-2x+1≥0
(1)若不等式对任意实数x恒成立,求实数m的取值范围;
(2)若不等式对任意x∈[2,4]恒成立,求实数m的取值范围.
(1)若不等式对任意实数x恒成立,求实数m的取值范围;
(2)若不等式对任意x∈[2,4]恒成立,求实数m的取值范围.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)根据一元二次不等式的性质可知,不等式(m-1)x2-2x+1≥0对任意实数x恒成立等价于
,求解即可得实数m的取值范围;
(2)构造函数f(x)=(m-1)x2-2x+1,根据二次函数性质,分情况讨论f(x)在x∈[2,4]时的最小值,解不等式f(x)min≥0即可确定实数m的取值范围.
|
(2)构造函数f(x)=(m-1)x2-2x+1,根据二次函数性质,分情况讨论f(x)在x∈[2,4]时的最小值,解不等式f(x)min≥0即可确定实数m的取值范围.
解答:
解:(1)∵不等式(m-1)x2-2x+1≥0对任意实数x恒成立,
∴
,
解得,m≥2
∴实数m的取值范围是[2,+∞).
(2)令f(x)=(m-1)x2-2x+1,
则f(x)图象关于x=
对称,
当m-1≤0时,f(x)在[2,4]上递减,f(4)=16(m-1)-7<0,
不满足题意;
当m-1>0时,若
≤2,则f(x)在[2,4]上递增,
不等式(m-1)x2-2x+1≥0对任意x∈[2,4]恒成立等价于
f(2)=4(m-1)-3≥0,
解得,m≥
;
若
≥4,则f(x)在[2,4]上递减,
不等式(m-1)x2-2x+1≥0对任意x∈[2,4]恒成立等价于
f(4)=16(m-1)-7≥0,
无解;
若2<
<4,则不等式(m-1)x2-2x+1≥0对任意x∈[2,4]恒成立等价于
△=4-4(m-1)≤0,无解.
综上所述,不等式对任意x∈[2,4]恒成立,实数m的取值范围是[
,+∞).
∴
|
解得,m≥2
∴实数m的取值范围是[2,+∞).
(2)令f(x)=(m-1)x2-2x+1,
则f(x)图象关于x=
| 1 |
| m-1 |
当m-1≤0时,f(x)在[2,4]上递减,f(4)=16(m-1)-7<0,
不满足题意;
当m-1>0时,若
| 1 |
| m-1 |
不等式(m-1)x2-2x+1≥0对任意x∈[2,4]恒成立等价于
f(2)=4(m-1)-3≥0,
解得,m≥
| 7 |
| 4 |
若
| 1 |
| m-1 |
不等式(m-1)x2-2x+1≥0对任意x∈[2,4]恒成立等价于
f(4)=16(m-1)-7≥0,
无解;
若2<
| 1 |
| m-1 |
△=4-4(m-1)≤0,无解.
综上所述,不等式对任意x∈[2,4]恒成立,实数m的取值范围是[
| 7 |
| 4 |
点评:本题考查的重点是恒成立问题,考查利用函数性质求函数的最值,解题的关键是构造函数求最值.属于难题.

练习册系列答案
相关题目
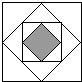 任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )
任意画一个正方形,再将这个正方体各边的中点相连得到第二个正方形,依此类推,这样一共画了4个正方形,如图所示.若向图形中随机投一点,则所投点落在第四个正方形的概率是( )