题目内容
已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=x2+2x.
(1)写出函数f(x)在x∈R的解析式;
(2)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
(1)写出函数f(x)在x∈R的解析式;
(2)若函数g(x)=f(x)-2ax+2(x∈[1,2]),求函数g(x)的最小值.
考点:函数奇偶性的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)根据函数f(x)是定义在R上的偶函数,f(-x)=f(x),且当x≥0时f(x)=x2+2x.可求出x<0时函数f(x)的解析式,综合可得函数f(x)的解析式
(2)根据(1)可得函数g(x)的解析式,结合二次函数的图象和性质,对a进行分类讨论,进而可得函数g(x)的最小值的表达式.
(2)根据(1)可得函数g(x)的解析式,结合二次函数的图象和性质,对a进行分类讨论,进而可得函数g(x)的最小值的表达式.
解答:
解:( 1)当x<0时,-x>0,
∵函数f(x)是偶函数,故f(-x)=f(x),且当x≥0时,f(x)=x2+2x…(2分)
所以f(x)=f(-x)=(-x)2+2(-x)=x2-2x,…(4分)
所以f(x)=
,
(2)∵g(x)=f(x)-2ax+2=x2+2(1-a)x+2的图象开口朝上且以直线x=a-1为对称,
又∵x∈[1,2],
当a-1≤1时,g(x)在[1,2]上为增函数,故当x=1时,g(x)取最小值5-2a,
当1<a-1≤2时,g(x)在[1,a-1]上为减函数,在[a-1,2]上为增函数,故当x=a-1时,g(x)取最小值-a2+2a+1,
当a-1>2时,g(x)在[1,2]上为减函数,故当x=2时,g(x)取最小值10-4a,
综上:函数g(x)的最小值为
∵函数f(x)是偶函数,故f(-x)=f(x),且当x≥0时,f(x)=x2+2x…(2分)
所以f(x)=f(-x)=(-x)2+2(-x)=x2-2x,…(4分)
所以f(x)=
|
(2)∵g(x)=f(x)-2ax+2=x2+2(1-a)x+2的图象开口朝上且以直线x=a-1为对称,
又∵x∈[1,2],
当a-1≤1时,g(x)在[1,2]上为增函数,故当x=1时,g(x)取最小值5-2a,
当1<a-1≤2时,g(x)在[1,a-1]上为减函数,在[a-1,2]上为增函数,故当x=a-1时,g(x)取最小值-a2+2a+1,
当a-1>2时,g(x)在[1,2]上为减函数,故当x=2时,g(x)取最小值10-4a,
综上:函数g(x)的最小值为
|
点评:本题考查的知识点是函数奇偶性的性质,函数解析式的求法,二次函数在定区间上的最值问题,是二次函数图象与性质与奇偶性的综合考查,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
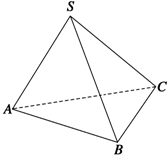 如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3,三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3,类比三角形中的正弦定理,给出空间情形的一个猜想.
如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3,三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3,类比三角形中的正弦定理,给出空间情形的一个猜想.