题目内容
已知数列{an}的前n项和为Sn,且满足a1=
,an=-2SnSn-1(n≥2).
(1)求S1,S2,S3;
(2)求数列{an}的通项公式;
(3)求证:S12+S22+S32+…+Sn2≤
-
.
| 1 |
| 2 |
(1)求S1,S2,S3;
(2)求数列{an}的通项公式;
(3)求证:S12+S22+S32+…+Sn2≤
| 1 |
| 2 |
| 1 |
| 4n |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)利用a1=
,an=-2SnSn-1,代入计算,可得S1,S2,S3;
(2)确定{
}是以2为首项,2为公差的等差数列,可得Sn=
,即可求数列{an}的通项公式;
(3)Sn2=
<
(
-
)(n≥2),利用叠加法,即可得出结论.
| 1 |
| 2 |
(2)确定{
| 1 |
| Sn |
| 1 |
| 2n |
(3)Sn2=
| 1 |
| 4n2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
解答:
(1)解:∵a1=
,an=-2SnSn-1,
∴S1=
,S2=
,S3=
;
(2)解:∵an=-2SnSn-1(n≥2),
∴Sn-Sn-1=-2SnSn-1,
∴
-
=2,
∴{
}是以2为首项,2为公差的等差数列.
∴
=2n,
∴Sn=
,
∴n≥2时,an=
,
∴an=
(3)证明:∵Sn2=
<
(
-
)(n≥2)
∴n≥2时,S12+S22+S32+…+Sn2<
+
(1-
+
-
+
-
)=
-
,
n=1时,S12=
-
,
综上,S12+S22+S32+…+Sn2≤
-
.
| 1 |
| 2 |
∴S1=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
(2)解:∵an=-2SnSn-1(n≥2),
∴Sn-Sn-1=-2SnSn-1,
∴
| 1 |
| Sn |
| 1 |
| Sn-1 |
∴{
| 1 |
| Sn |
∴
| 1 |
| Sn |
∴Sn=
| 1 |
| 2n |
∴n≥2时,an=
| 1 |
| 2n-2n2 |
∴an=
|
(3)证明:∵Sn2=
| 1 |
| 4n2 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
∴n≥2时,S12+S22+S32+…+Sn2<
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 4n |
n=1时,S12=
| 1 |
| 2 |
| 1 |
| 4•1 |
综上,S12+S22+S32+…+Sn2≤
| 1 |
| 2 |
| 1 |
| 4n |
点评:本题考查数列的通项与求和,考查数列与不等式的综合,考查学生分析解决问题的能力,确定数列的通项是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

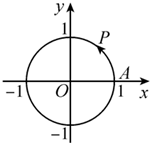 如图,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转.已知点P在1秒钟内转过的角度为θ(0<θ<π),经过2秒钟到达第三象限,经过14秒钟后又恰好回到出发点A,则θ=
如图,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转.已知点P在1秒钟内转过的角度为θ(0<θ<π),经过2秒钟到达第三象限,经过14秒钟后又恰好回到出发点A,则θ=