题目内容
2.某同学在求函数y=lgx和$y=\frac{1}{x}$的图象的交点时,计算出了下表所给出的函数值,则交点的横坐标在下列哪个区间内( )| x | 2 | 2.125 | 2.25 | 2.375 | 2.5 | 2.625 | 2.75 | 2.875 | 3 |
| lgx | 0.301 | 0.327 | 0.352 | 0.376 | 0.398 | 0.419 | 0.439 | 0.459 | 0.477 |
| $\frac{1}{x}$ | 0.5 | 0.471 | 0.444 | 0.421 | 0.400 | 0.381 | 0.364 | 0.348 | 0.333 |
| A. | (2.125,2,25) | B. | (2.75,2.875) | C. | (2.625,2.75) | D. | (2.5,2.625) |
分析 设f(x)=lgx-$\frac{1}{x}$,易知函数f(x)为增函数,求出f(2.5)f(2.625)<0,根据函数零点存在定理即可判断.
解答 解:设f(x)=lgx-$\frac{1}{x}$,
则f(2.5)=0.398-0.400<0,
f(2.625)=0.419-0.381>0,
∴f(2.5)f(2.625)<0,
∴函数f(x)=lgx-$\frac{1}{x}$的零点在(2.5,2.625)上,
∴y=lgx和$y=\frac{1}{x}$的图象的交点的横坐标在(2.5,2.625)上,
故选:D.
点评 本题考查了函数零点存在定理以及函数和图象的交点与函数零点的关系,属于基础题.

练习册系列答案
相关题目
10.经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为( )
| A. | 120° | B. | 150° | C. | 60° | D. | 30° |
14.已知p:x2-2x-3<0,q:x+2≥0,则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.正弦函数y=sinx的图象上最高点和最低点之间的最短距离是( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{4+{π}^{2}}$ | D. | 2$\sqrt{1+{π}^{2}}$ |
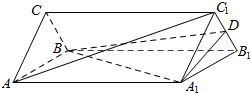 如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.
如图,底面为正三角形的三棱柱ABC-A1B1C1中,侧棱垂直于底面,D为线段B1C1中点.