题目内容
15.(1)已知$tanβ=\frac{1}{2}$,求sin2β-3sinβcosβ+4cos2β的值.(2)求函数定义域:$y=\sqrt{-2{{cos}^2}x+3cosx-1}+lg(36-{x^2})$.
分析 (1)利用“弦化切”的思想,sin2β-3sinβcosβ+4cos2β=$\frac{si{n}^{2}β-3sinβcosβ+4co{s}^{2}β}{si{n}^{2}β+co{s}^{2}β}$,同时除以cosβ,可转化为tanβ,可得答案.
(2)根据函数有意义,被开方数≥0,对数的真数>0,求解即可.
解答 解:(1)由sin2β-3sinβcosβ+4cos2β=$\frac{si{n}^{2}β-3sinβcosβ+4co{s}^{2}β}{si{n}^{2}β+co{s}^{2}β}$=$\frac{ta{n}^{2}β-tanβ+4}{ta{n}^{2}β+1}$
∵$tanβ=\frac{1}{2}$,
∴sin2β-3sinβcosβ+4cos2β=$\frac{\frac{1}{4}-\frac{1}{2}+4}{\frac{1}{4}+1}$=3.
(2)函数$y=\sqrt{-2{{cos}^2}x+3cosx-1}+lg(36-{x^2})$.
其定义域满足:$\left\{\begin{array}{l}{2co{s}^{2}x-3cosx+1≤0}\\{36-{x}^{2}>0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{\frac{1}{2}≤cosx≤1}\\{-6<x<6}\end{array}\right.$,
从而有:$\left\{\begin{array}{l}{2πk≤x≤\frac{π}{3}+2kπ,k∈Z}\\{-6<x<6}\end{array}\right.$,
∴函数定义域为(-6,$-\frac{5π}{3}$]∪[0,$\frac{π}{3}$]
点评 本题考查了“弦化切”及同角三角函数基本关系式,考查了计算能力,属于基础题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 8 |
| A. | 3 | B. | -$\frac{3}{2}$ | C. | $\frac{1}{3}$ | D. | -$\frac{2}{3}$ |
| A. | -2或-1 | B. | 1或2 | C. | ±$\sqrt{3}$或-1 | D. | ±1或2 |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
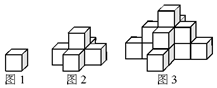 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )
图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第六个叠放的图形中,小正方体木块总数就是( )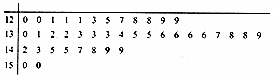 在高三某次数学测试中,40名优秀学生的成绩如图所示:
在高三某次数学测试中,40名优秀学生的成绩如图所示: