题目内容
12.已知点A(1,1),B(2,1),C(1,2),若-1≤λ≤2,2≤μ≤3,则$|{λ\overrightarrow{AB}+μ\overrightarrow{AC}}|$的取值范围是( )| A. | [1,10] | B. | $[{\sqrt{5},\sqrt{13}}]$ | C. | [1,5] | D. | $[{2,\sqrt{13}}]$ |
分析 用坐标表示出λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$以及模长,根据λ、μ的取值范围,转化为不等式组表示的平面区域内的点到原点的距离最值问题,即可求出答案.
解答 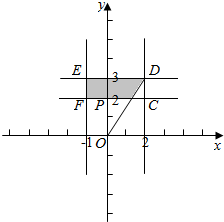 解:∵$\overrightarrow{AB}$=(1,0),$\overrightarrow{AC}$=(0,1),
解:∵$\overrightarrow{AB}$=(1,0),$\overrightarrow{AC}$=(0,1),
∴λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$=(λ,μ),
∴|λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$|=$\sqrt{{λ}^{2}{+μ}^{2}}$;
又∵-1≤λ≤2,2≤μ≤3,
∴λ、μ满足不等式组$\left\{\begin{array}{l}{-1≤λ≤2}\\{2≤μ≤3}\end{array}\right.$,
作出不等式组对应的平面区域,得到如图所示的矩形CDEF及其内部区域,
其中C(2,2),D(2,3),E(-1,3),F(-1,2),
则区域内的点到原点的距离最小值为|OP|=2,
最大值为|OD|=$\sqrt{{2}^{2}{+3}^{2}}$=$\sqrt{13}$;
∴$|{λ\overrightarrow{AB}+μ\overrightarrow{AC}}|$的取值范围是[2,$\sqrt{13}$].
故选:D.
点评 本题考查了平面向量的坐标应用问题,也考查了线性规划的应用问题,是综合性题目.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
17.设条件p:2x2-3x+1>0,条件q:$\frac{1}{x}$<1,则¬p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
7.已知$U=\{y|y={2^x},x≥-1\},A=\{x|\frac{1}{x-1}≥1\}$,则∁UA=( )
| A. | $[\frac{1}{2},2]$ | B. | [2,+∞) | C. | $[\frac{1}{2},1]∪(2,+∞)$ | D. | $[\frac{1}{2},2)∪(2,+∞)$ |
17.某校高安文科600名学生参加了12月的模拟考试,学校为了了解高三文科学生的数学、外语请客,利用随机数表法从抽取100名学生的成绩进行统计分析,将学生编号为000,001,002,…599
(1)若从第6行第7列的数开始右读,请你一次写出最先抽出的5个人的编号(下面是摘自随机数表的第4恒值第7行);
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(2)抽出的100名学生的数学、外语成绩如下表:
若数学成绩优秀率为35%,求m,n的值;
(3)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
(1)若从第6行第7列的数开始右读,请你一次写出最先抽出的5个人的编号(下面是摘自随机数表的第4恒值第7行);
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(2)抽出的100名学生的数学、外语成绩如下表:
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(3)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
4.王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的130网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍,若要用联通130应最少打多长时间的长途电话才合算.( )
| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲:联通130 | 12元 | 0.36元/分 | 0.06元/秒 |
| 乙:移动“神州行” | 无 | 0.60元/分 | 0.07元/秒 |
| A. | 300秒 | B. | 400秒 | C. | 500秒 | D. | 600秒 |
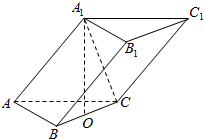 如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.
如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.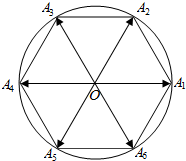 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.