题目内容
在△ABC中，a+b=2
，ab=2，且角C的度数为120°
（1）求△ABC的面积；
（2）求边c的长．
| 3 |
（1）求△ABC的面积；
（2）求边c的长．
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）直接根据三角形的面积公式即可求△ABC的面积；
（2）根据余弦定理，利用条件即可求边c的长．
（2）根据余弦定理，利用条件即可求边c的长．
解答：
解：（1）∵ab=2，且角C的度数为120°
∴S=
absinC=
．
（2）∵c2=a2+b2-2abcosC=（a+b）2-2ab（cosC+1）=12-2=10．
∴c=
．
∴S=
| 1 |
| 2 |
| ||
| 2 |
（2）∵c2=a2+b2-2abcosC=（a+b）2-2ab（cosC+1）=12-2=10．
∴c=
| 10 |
点评：本题主要考查三角形的面积公式的计算，以及余弦定理的应用，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
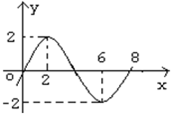函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+…+f（11）的值是（ ）A、2+2
| ||
B、2-2
| ||
| C、0 | ||
| D、-1 |
方程sinx=-cos80°的解集是（ ）
| A、{X|X=k•180°+10°，k∈z} |
| B、{x|x=k•360°+10°，k∈z} |
| C、{x|x=k•180°±10°，k∈z} |
| D、{x|x=k•180°-（-1）k•10°，k∈z} |