题目内容
9．数列{an}的前n项和Sn=33n-n2．（1）求数列{an}的通项公式；
（2）求证：{an}是等差数列．
分析 （1）根据≥2时，an=Sn-Sn-1，即可求出通项公式，
（2）再利用定义证明即可．
解答 解 （1）当n≥2时，an=Sn-Sn-1=34-2n，
又当n=1时，a1=S1=32=34-2×1满足an=34-2n．
故{an}的通项为an=34-2n．
（2）证明：an+1-an=34-2（n+1）-（34-2n）=-2．
故数列{an}是以32为首项，-2为公差的等差数列．
点评 本题考查了数列的递推关系式，以及等差数列的定义，属于基础题．
练习册系列答案
口算能手系列答案
相关题目
20．已知函数$y=|{sin（{2x-\frac{π}{6}}）}|$，以下说法正确的是（ ）
| A． | 函数的最小正周期为$\frac{π}{4}$ | B． | 函数是偶函数 | ||
| C． | 函数图象的一条对称轴为$x=\frac{π}{3}$ | D． | 函数在$[{\frac{2π}{3}，\frac{5π}{6}}]$上为减函数 |
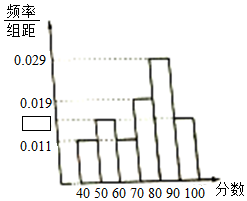为了解某社区物业部门对本小区业主的服务情况，随机访问了100位业主，根据这100位业主对物业部门的评分情况，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．由于某种原因，有个数据出现污损，请根据图中其他数据分析，评分不小于80分的业主有（ ）位．
1．已知圆${（x-1）^2}+{y^2}=\frac{3}{4}$的一条切线y=kx与双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$没有公共点，则双曲线C的离心率的取值范围是（ ）
| A． | $（1，\sqrt{3}）$ | B． | （1，2] | C． | $（\sqrt{3}，+∞）$ | D． | [2，+∞） |