题目内容
(本小题满分14分)
已知椭圆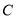 的两个焦点的坐标分别为
的两个焦点的坐标分别为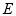
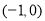 ,
,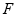
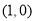 ,并且经过点(
,并且经过点(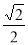 ,
,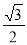 ),M、N为椭圆
),M、N为椭圆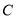 上关于
上关于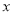 轴对称的不同两点.
轴对称的不同两点.
(1)求椭圆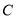 的标准方程;
的标准方程;
(2)若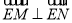 ,试求点
,试求点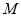 的坐标;
的坐标;
(3)若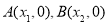 为
为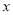 轴上两点,且
轴上两点,且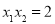 ,试判断直线
,试判断直线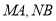 的交点
的交点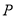 是否在椭圆
是否在椭圆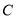 上,并证明你的结论.
上,并证明你的结论.
(1)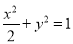
(2)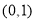 、
、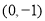 、
、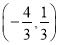 、
、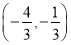
(3)在,答案见解析.
【解析】
试题分析:第一问求椭圆的方程,可以应用待定系数法求解,也可以应用椭圆的定义来求,用椭圆所过的一个点到两个焦点的距离为2a来求解,第二问,通过向量的数量积等于0和点在椭圆上,找出点的坐标所满足的方程组,从而得结果,第二问注意垂直关系由向量的数量积等于0来体现,第三问注意判断点在曲线上的条件可以由点的坐标满足方程来体现.
试题解析:(1)依定义,椭圆的长轴长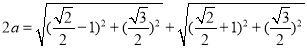 ,(1分)
,(1分)
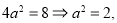 又
又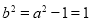 , (3分)
, (3分)
因此,所求的椭圆标准方程为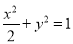 . (4分)
. (4分)
或:设椭圆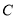 的标准方程为
的标准方程为 (1分)
(1分)
因为点(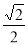 ,
,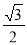 )在椭圆上,所以
)在椭圆上,所以 又
又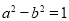 (3分)
(3分)
解得 
因此,所求的椭圆标准方程为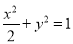 . (4分)
. (4分)
(2)设 ,
,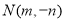 ,则
,则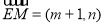 ,
,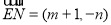 ,(5分)
,(5分)
因为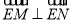 , 所以
, 所以 ,即
,即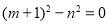 ①, (6分)
①, (6分)
因为点 在椭圆
在椭圆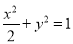 上,所以
上,所以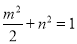 ② (7分)
② (7分)
由①②解得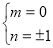 ,或
,或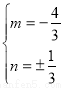 . (8分)
. (8分)
因此,符合条件的点有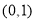 、
、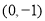 、
、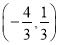 、
、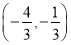 . (9分)
. (9分)
(3)设 ,则直线
,则直线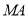 、
、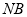 的方程分别为
的方程分别为
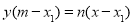 ③,
③,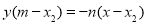 ④ (10分)
④ (10分)
设直线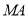 与直线
与直线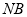 交点为P
交点为P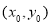 ,将其坐标代人③、④并整理,得
,将其坐标代人③、④并整理,得
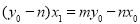 ⑤ ,
⑤ ,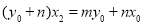 ⑥ (11分)
⑥ (11分)
⑤与⑥相乘得 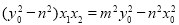 ⑦, (12分)
⑦, (12分)
又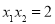 ,
,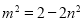 ,代入⑦化简得
,代入⑦化简得 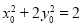 . (13分)
. (13分)
因此,直线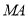 与直线
与直线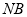 的交点
的交点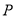 仍在椭圆
仍在椭圆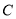 上. (14分)
上. (14分)
考点:椭圆的标准方程,向量垂直的等量关系,点在曲线上的判定方法.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案 和不共线的三点
和不共线的三点 、
、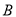 、
、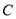 有
有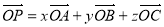 ,则
,则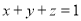 是四点
是四点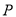 、
、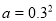 ,
, ,
,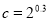 之间的大小关系是( )
之间的大小关系是( ) 中,已知
中,已知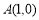 ,
,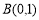 ,点C在第一象限内,
,点C在第一象限内,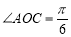 ,且
,且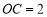 ,若
,若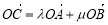 ,则
,则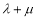 的值是__________.
的值是__________. ,
, 有零点,则m的取值范围是
有零点,则m的取值范围是



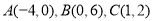 .
.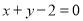 平行的直线方程;
平行的直线方程; 与平面
与平面 ,则下列四个命题中假命题是
,则下列四个命题中假命题是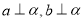 ,那么
,那么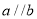 B.如果
B.如果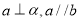 ,那么
,那么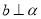
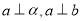 ,那么
,那么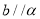 D.如果
D.如果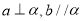 ,那么
,那么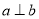
 且与
且与 有相同焦点的椭圆的方程是 .
有相同焦点的椭圆的方程是 .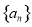 的前n项和为
的前n项和为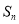 ,公差d≠0,且
,公差d≠0,且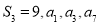 成等比数列.
成等比数列.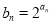 ,求数列{
,求数列{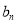 }的前n项和
}的前n项和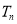 .
.