题目内容
(本小题满分12分)已知等差数列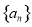 的前n项和为
的前n项和为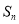 ,公差d≠0,且
,公差d≠0,且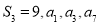 成等比数列.
成等比数列.
(1)求数列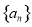 的通项公式;
的通项公式;
(2)设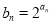 ,求数列{
,求数列{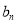 }的前n项和
}的前n项和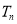 .
.
(1) =n+1;(2)
=n+1;(2)
【解析】
试题分析:(1) ,即
,即 ,化简得
,化简得 ,d=0(舍去).
,d=0(舍去).
∴ ,得
,得 =2,d=1.
=2,d=1.
∴ =
= +(n-1)d=2+(n-1)=n+1,即
+(n-1)d=2+(n-1)=n+1,即 =n+1.
=n+1.
(2)∵ =
= ,∴
,∴ =4,
=4, .
.
∴{ }是以4为首项,2为公比的等比数列,
}是以4为首项,2为公比的等比数列,
∴
考点:本题考查等差数列的前n项和公式,等差数列通项公式,等比数列前n项和公式
点评:解决本题的关键是熟练掌握等差数列通项公式和前n项和公式,等比数列前n项和公式

练习册系列答案
相关题目
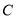 的两个焦点的坐标分别为
的两个焦点的坐标分别为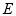
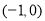 ,
,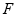
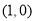 ,并且经过点(
,并且经过点(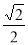 ,
,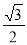 ),M、N为椭圆
),M、N为椭圆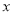 轴对称的不同两点.
轴对称的不同两点.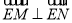 ,试求点
,试求点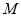 的坐标;
的坐标;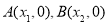 为
为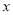 轴上两点,且
轴上两点,且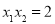 ,试判断直线
,试判断直线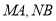 的交点
的交点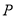 是否在椭圆
是否在椭圆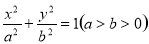 的左焦点
的左焦点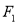 坐标为
坐标为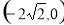 ,且椭圆C的短轴长为4,斜率为1的直线
,且椭圆C的短轴长为4,斜率为1的直线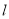 与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为
与椭圆G交于A,B两点,以AB为底边的等腰三角形,顶点为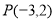 .
.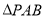 的面积
的面积 中,已知
中,已知 ,则数列
,则数列 为( )
为( ) C.2 D.
C.2 D.

 在R上的部分图像如图所示,则
在R上的部分图像如图所示,则
 .
.
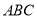 中,角
中,角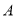
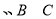 所对应的边分别为
所对应的边分别为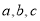 ,若
,若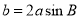 ,则角
,则角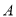 等于( )
等于( )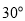 B.
B.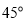 C.
C.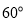 D.
D.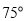
 的终边过点
的终边过点 ,那么
,那么 .
. _________.
_________.