题目内容
已知10件不同的产品中共有3件次品,现对它们进行一一测试,直到找出所有3件次品为止.
(1)求恰好在第5次测试时3件次品全部被测出的概率;
(2)记恰好在第k次测试时3件次品全部被测出的概率为f(k),求f(k)的最大值和最小值.
(1)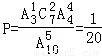
(2)故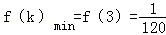 ,
,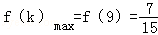 .
.
【解析】
试题分析:(1)根据题意,若恰好在第5次测试时3件次品全部被测出,则第5次取出第3件次品,前4次中有2次是次品,2次是正品;有排列、组合数公式可得其情况数目,易得从10件产品中顺序取出5件的情况数目,由等可能事件的概率,计算可得答案;
(2)根据题意,分析可得k的范围是3≤k≤9,进而分3≤k≤6、7≤k≤9时讨论,由等可能事件计算可得f(k),比较大小可得答案.
【解析】
(1)若恰好在第5次测试时3件次品全部被测出,则第5次取出第3件次品,前4次中有2次是次品,2次是正品;
则有A31C72A44种情况,从10件产品中顺序取出5件,有A105种情况,
则第5次测试时3件次品全部被测出的概率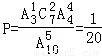 ,
,
(2)根据题意,分析可得k的范围是3≤k≤9,
当3≤k≤6时,若恰好在第k次测试时3件次品全部被测出,则第k次取出第3件次品,前k﹣1次中有2次是次品,k﹣3次是正品;而从10件产品中顺序取出k件,有A10k种情况,则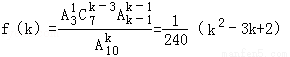 ,
,
则f(3)=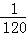 ,f(4)=
,f(4)= ,f(5)=
,f(5)=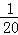 ,f(6)=
,f(6)=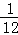 ;
;
当k=7时,即恰好在第7次测试时3件次品全部被测出,有两种情况,一是第7次取出第3件次品,前6次中有2次是次品,4次是正品;二是前7次没有取出次品,此时也可以测出三件次品,
则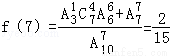 ;
;
当k=8时,即恰好在第7次测试时3件次品全部被测出,有两种情况,一是第8次取出第3件次品,前7次中有2次是次品,5次是正品;二是前7次恰有一次次品,第8次取出为合格品,
则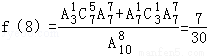 ;
;
当k=9时,即恰好在第9次测试时3件次品全部被测出,有两种情况,一是第9次取出第3件次品,前8次中有2次是次品,6次是正品;二是前8次取出1次次品,第9次取出第2件次品,
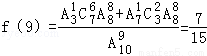 .
.
故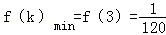 ,
,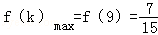 .
.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案 的图像向右平移
的图像向右平移 个单位,再向上平移
个单位,再向上平移 个单位,
个单位,


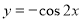
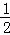 B.
B.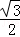 C.
C.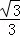 D.
D.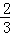
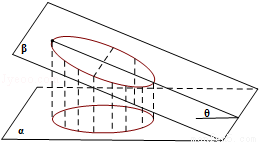
 ,则B、C两点的球面距离是( )
,则B、C两点的球面距离是( )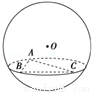
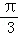 B.π C.
B.π C.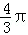 D.2π
D.2π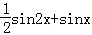 ,则f′(x)是( )
,则f′(x)是( )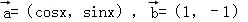 ,将函数
,将函数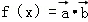 的图象按向量
的图象按向量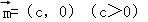 平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )
平移后,所得图象恰好为函数y=﹣f′(x)(f′(x)为f(x)的导函数)的图象,则c的值可以为( )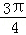 B.π C.
B.π C.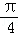 D.
D.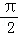
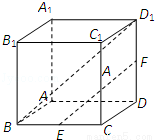
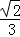 B.
B.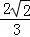 C.
C.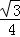 D.
D.