Question

19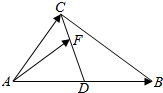．如图所示，在△ABC中，AD=DB，F在线段CD上的动点，设$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$，则$\frac{1}{x}+\frac{4}{y}$的最小值为（　　）

• A． 9
• B． 10
• C． $6+4\sqrt{2}$
• D． $9+4\sqrt{2}$

Answer 1

分析 根据C，F，D三点共线可得x，y的关系，再利用基本不等式解出．

解答 解：$\overrightarrow{AF}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$=2x$\overrightarrow{AD}$+y$\overrightarrow{b}$，∵C，F，D三点共线，∴2x+y=1．x＞0，y＞0．
∴$\frac{1}{x}+\frac{4}{y}$=$\frac{2x+y}{x}+\frac{4（2x+y）}{y}$=6+$\frac{y}{x}$+$\frac{8x}{y}$≥6+2$\sqrt{8}$=6$+4\sqrt{2}$．
当且仅当$\frac{y}{x}=\frac{8x}{y}$即y=2$\sqrt{2}$x时取等号．
故选：C．

点评 本题考查了向量共线定理和基本不等式的性质，属于基础题．