题目内容
14．“-2≤a≤2”是“一元二次方程x2+ax+1=0没有实根”的（ ）| A． | 充要条件 | B． | 必要非充分条件 | ||
| C． | 充分非必要条件 | D． | 非充分非必要条件 |
分析 一元二次方程x2+ax+1=0没有实根，则△＜0．解出即可判断出．
解答 解：若一元二次方程x2+ax+1=0没有实根，
则△=a2-4＜0．
解得-2＜a＜2．
∴“-2≤a≤2”是“一元二次方程x2+ax+1=0没有实根”必要不充分条件．
故选：B．
点评 本题考查了一元二次方程有实数根与判别式的关系、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
4．已知两条直线l1：y=m和l2：y=$\frac{9}{m}$（m＞0），l1与函数y=|log2x|的图象从左至右相交于点A，B，l2与函数y=|log2x|的图象从左至右相交于C，D．记线段AC和BD在x轴上的投影长度分别为a，b，当m变化时，$\frac{b}{a}$的最小值为（ ）
| A． | 32 | B． | $\frac{1}{64}$ | C． | 64 | D． | $\frac{1}{64}$ |
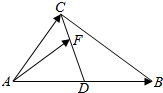如图所示，在△ABC中，AD=DB，F在线段CD上的动点，设$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$，则$\frac{1}{x}+\frac{4}{y}$的最小值为（ ）