题目内容
9.设A、B是直线3x+4y+3=0与圆x2+y2+4y=0的两个交点,则线段AB的垂直平分线的方程是4x-3y-6=0,弦长|AB|为2$\sqrt{3}$.分析 根根线段AB的垂直平分线过圆的圆心,且和直线AB垂直,求出圆心坐标和直线的斜率即可得到线段AB的垂直平分线的方程,求出圆心到直线AB的距离d,利用勾股定理,求出弦长|AB|.
解答 解:∵A、B是直线3x+4y+3=0与圆x2+y2+4y=0的两个交点,
∴线段AB的垂直平分线过圆的圆心,且和直线AB垂直,
则垂直平方线的斜率k=$\frac{4}{3}$,
圆的标准方程是x2+(y+2)2=4,
则圆心坐标为(0,-2),半径R=2,
则垂直平分线的方程为y+2=$\frac{4}{3}$x,即4x-3y-6=0,
圆心到直线AB的距离d=$\frac{|0-8+3|}{\sqrt{9+16}}$=1,∴|AB|=2$\sqrt{{2}^{2}-{1}^{2}}$=2$\sqrt{3}$.
故答案为:4x-3y-6=0,2$\sqrt{3}$.
点评 本题主要考查直线和圆的位置关系的应用,利用AB垂直平分线的性质是解决本题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
19.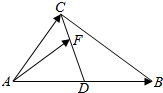 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )| A. | 9 | B. | 10 | C. | $6+4\sqrt{2}$ | D. | $9+4\sqrt{2}$ |
17.集合M={y|y=lg(x2+1),N={x|2x<4},则M∩N等于( )
| A. | [0,+∞) | B. | [0,2) | C. | (2,+∞) | D. | (0,2] |
4.设l,m,n为三条不同的直线,α为一个平面,下列命题中正确的是( )
①若l⊥α,则l与α相交
②若m?α,n?α,l⊥m,l⊥n,则l⊥α
③若l∥m,m∥n,l⊥α,则n⊥α
④若l∥m,m⊥α,n⊥α,则l∥n.
①若l⊥α,则l与α相交
②若m?α,n?α,l⊥m,l⊥n,则l⊥α
③若l∥m,m∥n,l⊥α,则n⊥α
④若l∥m,m⊥α,n⊥α,则l∥n.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
19.某制药公司研制出一种新流感疫苗,为测试该疫苗的有效性,公司选定3000个流感样本分成三组,测试结果如下表:
已知在全体样本中随机抽取1个,抽取B组的概率是$\frac{1}{3}$
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取600个测试结果,问应在C组抽取多少个?
(3)若疫苗有效的概率不小于99%,则认为测试通过,已知y≥885,求不能通过测试的概率.
| A组 | B组 | C组 | |
| 疫苗有效 | 903 | x | y |
| 疫苗无效 | 197 | 90 | z |
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取600个测试结果,问应在C组抽取多少个?
(3)若疫苗有效的概率不小于99%,则认为测试通过,已知y≥885,求不能通过测试的概率.