题目内容
8.(设全集是实数集R,A={x|2x2-7x+3≤0},B={x|x2+a<0},(1)当a=-4时,求A∩B和A∪B;
(2 若(∁RA)∩B=B,求负数a的取值范围.
分析 (1)当a=-4时,解一元二次不等式求得A 和B,再根据两个集合的并集的定义求得 A∪B.
(2)由(∁RA)∩B=B,可得 B⊆(∁RA).求得(∁RA)和 B,考查集合的端点值的大小关系可得$\sqrt{-a}$≤$\frac{1}{2}$,从而求得负数a的取值范围.
解答 解:(1)当a=-4时,A={x|2x2-7x+3≤0}={x|$\frac{1}{2}$≤x≤3},B={x|x2+a<0}={x|x2<4}={x|-2<x<2},
∴A∪B={x|-2<x≤3}.
(2)若(∁RA)∩B=B,则 B⊆(∁RA).又(∁RA)={x|x<$\frac{1}{2}$,或 x>3},且a<0,
∴B={x|-$\sqrt{-a}$<x<$\sqrt{-a}$},
∴$\sqrt{-a}$≤$\frac{1}{2}$,解得-$\frac{1}{4}$≤a<0,即负数a的取值范围为[-$\frac{1}{4}$,0).
点评 本题主要考查一元二次不等式的解法,两个集合的交集、并集、补集的运算,集合间的包含关系,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
19.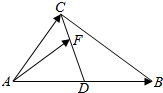 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )| A. | 9 | B. | 10 | C. | $6+4\sqrt{2}$ | D. | $9+4\sqrt{2}$ |
16.已知函数f(x)=|x+1|+|x-1|,则下列坐标表示的点一定在函数f(x)图象上的是( )
| A. | (-a,-f(a)) | B. | (-a,f(a)) | C. | (a,-f(a)) | D. | (a,-f(-a)) |
17.集合M={y|y=lg(x2+1),N={x|2x<4},则M∩N等于( )
| A. | [0,+∞) | B. | [0,2) | C. | (2,+∞) | D. | (0,2] |