题目内容
4.若函数$f(x)=\frac{x-1}{x+2}$在(-2,4)上的值域为$(-∞,\frac{1}{2})$.分析 函数f(x)=1-$\frac{3}{x+2}$,由于x∈(-2,4),利用反比例函数的单调性可得$\frac{3}{x+2}$∈$(\frac{1}{2},+∞)$,即可得出.
解答 解:函数$f(x)=\frac{x-1}{x+2}$=$\frac{x+2-3}{x+2}$=1-$\frac{3}{x+2}$,
∵x∈(-2,4),
∴$\frac{3}{x+2}$∈$(\frac{1}{2},+∞)$,
∴1-$\frac{3}{x+2}$∈$(-∞,\frac{1}{2})$,
∴函数$f(x)=\frac{x-1}{x+2}$在(-2,4)上的值域为∈$(-∞,\frac{1}{2})$,
故答案为:$(-∞,\frac{1}{2})$.
点评 本题考查了反比例函数的单调性,考查了变形能力与计算能力,属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
15.已知过点C(6,-8)作圆x2+y2=25的切线,切点分别为A,B,那么点C到直线AB的距离为( )
| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
19.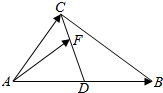 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
 如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )
如图所示,在△ABC中,AD=DB,F在线段CD上的动点,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,$\overrightarrow{AF}=x\overrightarrow a+y\overrightarrow b$,则$\frac{1}{x}+\frac{4}{y}$的最小值为( )| A. | 9 | B. | 10 | C. | $6+4\sqrt{2}$ | D. | $9+4\sqrt{2}$ |
16.已知函数f(x)=|x+1|+|x-1|,则下列坐标表示的点一定在函数f(x)图象上的是( )
| A. | (-a,-f(a)) | B. | (-a,f(a)) | C. | (a,-f(a)) | D. | (a,-f(-a)) |