题目内容
等比数列{an}的公比0<q<1,a172=a24,则使a1+a2+…+an>
+
+…+
成立的正整数n的最大值为 .
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:求出数列的前n项和,根据不等式之间的关系即可得到结论.
解答:
解:设首项为a1,公比为q,依题意有(a1q16)2=a1q23,
∴a1q9=1.则a1>0,且a1=q-9,
∵{an}为等比数列,∴{
}是以
为首项,
为公比的等比数列.
则不等式等价为
>
,
∵0<q<1,把a1=q-9,即a12=q-18代入整理,
得q-18(1-qn)>q1-n(1-qn),
∴q-18>q1-n,
∴-18<1-n,
即n<19,
∵n∈N*,∴n的最大值为18.
故答案为:18.
∴a1q9=1.则a1>0,且a1=q-9,
∵{an}为等比数列,∴{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| q |
则不等式等价为
| a1(1-qn) |
| 1-q |
| ||||
1-
|
∵0<q<1,把a1=q-9,即a12=q-18代入整理,
得q-18(1-qn)>q1-n(1-qn),
∴q-18>q1-n,
∴-18<1-n,
即n<19,
∵n∈N*,∴n的最大值为18.
故答案为:18.
点评:本题主要考查等比数列的通项公式和前n项和的应用,考查数列与不等式的应用,综合性较强,运算量较大.

练习册系列答案
相关题目
等比数列{an]中,“a1<a3”是“a4<a6”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
“m<0”是“方程x2+my2=1表示双曲线”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在长为8的线段AB上任取一点C,现作一矩形,邻边长分别等于AC、BC的长,则该矩形面积大于15的概率( )
A、
| ||
B、
| ||
C、
| ||
D、
|
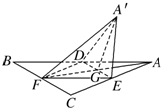 如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
如图,正三角形ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题: