题目内容
已知函数f(x)=ax3+bx2-3x+a+2b-1是R上的奇函数.
(1)求函数f(x)的解析式;
(2)求f′(2)+f′(-2)的值;
(3)求函数f(x)的单调区间.
(1)求函数f(x)的解析式;
(2)求f′(2)+f′(-2)的值;
(3)求函数f(x)的单调区间.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)首先,根据f(-x)=-f(x),得到2bx2+2(a+2b-1)=0,然后,求解即可;
(2)首先,求解导数,然后,求解其值;
(3)直接结合导数求解其单调区间即可.
(2)首先,求解导数,然后,求解其值;
(3)直接结合导数求解其单调区间即可.
解答:
解:(1)∵函数f(x)=ax3+bx2-3x+a+2b-1是R上的奇函数,
∴f(-x)=-f(x),
∴2bx2+2(a+2b-1)=0,
∴
,
∴
,
∴f(x)=x3-3x.
(2)根据(1)得
f′(x)=3x2-3,
∴f′(2)=9,f′(-2)=9,
∴f′(2)+f′(-2)=18,
(3)令f′(x)=3x2-3>0,
∴x<-1 或 x>1,
∴单调增区间为:(-∞,-1),(1,+∞),
令f′(x)=3x2-3<0,
∴-1<x<1,
∴单调减区间为:(-1,1).
∴f(-x)=-f(x),
∴2bx2+2(a+2b-1)=0,
∴
|
∴
|
∴f(x)=x3-3x.
(2)根据(1)得
f′(x)=3x2-3,
∴f′(2)=9,f′(-2)=9,
∴f′(2)+f′(-2)=18,
(3)令f′(x)=3x2-3>0,
∴x<-1 或 x>1,
∴单调增区间为:(-∞,-1),(1,+∞),
令f′(x)=3x2-3<0,
∴-1<x<1,
∴单调减区间为:(-1,1).
点评:本题重点考查了函数的单调性和奇偶性等知识,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
函数f(x)=x-3+log3x的零点所在的区间是( )
| A、(0,1) |
| B、(1,3) |
| C、(-∞,0) |
| D、(3,+∞) |
函数y=x2-4x+10在区间[1,4)上( )
| A、最小值是6,最大值是10 |
| B、最小值是7,最大值是10 |
| C、最小值是6,没有最大值 |
| D、最小值是7,没有最大值 |
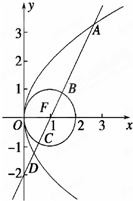 已知抛物线M:y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下依次与上述两曲线交于点A,B,C,D(如图所示),T(-1,0).
已知抛物线M:y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下依次与上述两曲线交于点A,B,C,D(如图所示),T(-1,0).