题目内容
椭圆
+
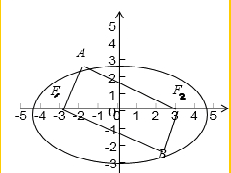
=1（a＞b＞0）上一点A关于原点的对称点为B，!F为其左焦点，若AF⊥BF，设∠ABF=
，则该椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|
考点：椭圆的简单性质
专题：数形结合,圆锥曲线的定义、性质与方程
分析：根据对称性得出四边形AF2BF1为矩形，设AF1=x，则BF1=
x，运用矩形的几何性质，得出边长，
再运用定义判断得出（
+1）c=2a，即可求解离心率．
| 3 |
再运用定义判断得出（
| 3 |
解答：
解：椭圆
+
=1（a＞b＞0）上一点A关于原点的对称点为B，
F1（-c，0），F2（c，0）A（x0，y0），B（-x0，-y0），
∵AF⊥BF，设∠ABF=
，
∴根据椭圆的对称性可知：四边形AF2BF1为矩形，
∴∴AF2=BF1=
x，F1F2=2x
∴x+
x=2a．F1F2=2c=2x，
∴（
+1）c=2a，
∴
=
=
-1
| x2 |
| a2 |
| y2 |
| b2 |
F1（-c，0），F2（c，0）A（x0，y0），B（-x0，-y0），
∵AF⊥BF，设∠ABF=
| π |
| 6 |
∴根据椭圆的对称性可知：四边形AF2BF1为矩形，
∴∴AF2=BF1=
| 3 |
∴x+
| 3 |
∴（
| 3 |
∴
| c |
| a |
| 2 | ||
|
| 3 |
点评：本题考察了椭圆的几何性质，定义，解直角三角形，矩形的几何性质，运用数形结合数学解决代数问题，属于中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
函数y=ax+1（a＞0且a≠1）的图象必经过点（ ）
| A、（0，1） |
| B、（1，0） |
| C、（2，1） |
| D、（0，2） |
设集合M={-1，0，1}，N={x|x2≤x}，M∩N=（ ）
| A、{0} |
| B、{0，1} |
| C、{-1，1} |
| D、{-1，0} |
已知c是椭圆C：
+
=1(a＞b＞0)的半焦距，则
的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| a |
| b+c |
A、[
| ||||
B、[
| ||||
C、(0，
| ||||
D、(
|
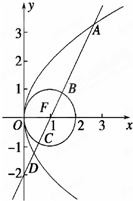已知抛物线M：y2=4x，圆F：（x-1）2+y2=1，过点F作直线l，自上而下依次与上述两曲线交于点A，B，C，D（如图所示），T（-1，0）．