题目内容
下列命题中:
①命题“若x2-3x+2=0,则x=1”的否命题为“若x2-3x+2=0,则x≠1”;
②命题“若方程x2-mx+1=0有解,则m>4”的逆命题为真命题;
③对命题p和q,“p且q为假”是“p或q为假”的必要不充分条件.
假命题的序号为 .
①命题“若x2-3x+2=0,则x=1”的否命题为“若x2-3x+2=0,则x≠1”;
②命题“若方程x2-mx+1=0有解,则m>4”的逆命题为真命题;
③对命题p和q,“p且q为假”是“p或q为假”的必要不充分条件.
假命题的序号为
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接写出原命题的否命题判断①;由m>4时方程x2-mx+1=0的判别式为m2-4>0,方程有解判断②;
由复合命题的真值表判断③.
由复合命题的真值表判断③.
解答:
解:对于①,命题“若x2-3x+2=0,则x=1”的否命题为“若x2-3x+2≠0,则x≠1”,命题①为假命题;
对于②,命题“若方程x2-mx+1=0有解,则m>4”的逆命题为“若m>4,则方程x2-mx+1=0有解”
∵m>4时方程x2-mx+1=0的判别式为m2-4>0,方程有解,
∴命题②为真命题;
③对命题p和q,若p且q为假,则p,q中至少一个为假,p或q不一定为假,若p或q为假,则p,q均为假,
∴“p且q为假”是“p或q为假”的必要不充分条件,命题③为真命题.
故答案为:①.
对于②,命题“若方程x2-mx+1=0有解,则m>4”的逆命题为“若m>4,则方程x2-mx+1=0有解”
∵m>4时方程x2-mx+1=0的判别式为m2-4>0,方程有解,
∴命题②为真命题;
③对命题p和q,若p且q为假,则p,q中至少一个为假,p或q不一定为假,若p或q为假,则p,q均为假,
∴“p且q为假”是“p或q为假”的必要不充分条件,命题③为真命题.
故答案为:①.
点评:本题考查了命题的真假判断与应用,考查了命题真假的判断方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两异面直线a,b的夹角是15°,过空间一点P作直线l,使得l与a,b的夹角均为8°,那么这样的直线l有( )
| A、3条 | B、2条 | C、1条 | D、0条 |
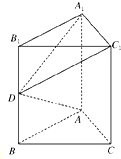 如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.
如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.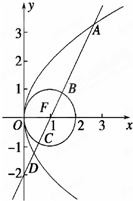 已知抛物线M:y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下依次与上述两曲线交于点A,B,C,D(如图所示),T(-1,0).
已知抛物线M:y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下依次与上述两曲线交于点A,B,C,D(如图所示),T(-1,0). 某几何体三视图如图所示,其中正视图和侧视图都是等腰梯形,且上底长为2,下底长为4,腰长为
某几何体三视图如图所示,其中正视图和侧视图都是等腰梯形,且上底长为2,下底长为4,腰长为