题目内容
为了调查我市在校中学生参加体育运动的情况,从中随机抽取了16名男同学和14名女同学,调查发现,男、女同学中分别有12人和6人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关?
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为ξ,求ξ的分布列和均值.参考数据:
(1)根据以上数据完成以下2×2列联表:
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 16 | ||
| 女 | 14 | ||
| 总计 | 30 |
(3)将以上统计结果中的频率视作概率,从我市中学生中随机抽取3人,若其中喜爱运动的人数为ξ,求ξ的分布列和均值.参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
考点:独立性检验的应用,离散型随机变量的期望与方差
专题:综合题,概率与统计
分析:(1)本题是一个简单的数字的运算,根据a,b,c,d的已知和未知的结果,做出空格处的结果.
(2)假设是否喜爱运动与性别无关,由已知数据可求得观测值,把求得的观测值同临界值进行比较,得到在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关.
(3)喜爱运动的人数为ξ,ξ的取值分别为0,1,2,3,结合变量对应的事件利用等可能事件的概率公式做出概率,写出分布列和期望.
(2)假设是否喜爱运动与性别无关,由已知数据可求得观测值,把求得的观测值同临界值进行比较,得到在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关.
(3)喜爱运动的人数为ξ,ξ的取值分别为0,1,2,3,结合变量对应的事件利用等可能事件的概率公式做出概率,写出分布列和期望.
解答:
解:(1)
…(2分)
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:K2=
≈3.2143<6.635…..(5分)
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关….(6分)
(3)统计结果中喜爱运动的中学生所占的频率为
.…..(7分)
喜爱运动的人数为ξ的取值分别为:0,1,2,3,则有:P(ξ=0)=
(
)0(
)3=
P(ξ=1)=
•(
)2=
P(ξ=2)=
•(
)2=
P(ξ=3)=
(
)3=
….(10分)
喜爱运动的人数为ξ的分布列为:
…(11分)
因为ξ~B(3,
),所以喜爱运动的人数ξ的值为 Eξ=3×
=
….(12分)
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 12 | 4 | 16 |
| 女 | 6 | 8 | 14 |
| 总计 | 18 | 12 | 30 |
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:K2=
| 30×(12×8-6×4)2 |
| (12+4)(6+8)(12+6)(4+8) |
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关….(6分)
(3)统计结果中喜爱运动的中学生所占的频率为
| 3 |
| 5 |
喜爱运动的人数为ξ的取值分别为:0,1,2,3,则有:P(ξ=0)=
| C | 0 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 8 |
| 125 |
| C | 1 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 36 |
| 125 |
| C | 2 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 54 |
| 125 |
| C | 3 3 |
| 3 |
| 5 |
| 27 |
| 125 |
….(10分)
喜爱运动的人数为ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
因为ξ~B(3,
| 3 |
| 5 |
| 3 |
| 5 |
| 9 |
| 5 |
点评:本题考查独立性检验的应用,考查离散型随机变量的分布列和期望,是一个综合题,准确的数据运算是解决问题的关键.

练习册系列答案
相关题目
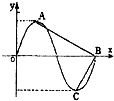 已知函数f(x)=
已知函数f(x)=| 3 |
| A、周期为4的奇函数 |
| B、周期为4的偶函数 |
| C、周期为2π的非奇非偶函数 |
| D、周期为4的非奇非偶函数 |
定义在R上的函数f(x)满足f(0)=0,f(x)+f(1-x)=1,f(
)=
f(x),且当0≤x1<x2≤1时,f(x1)≤f(x2),则f(
)的值为( )
| x |
| 3 |
| 1 |
| 2 |
| 1 |
| 2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
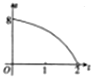
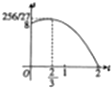
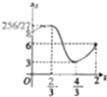
 如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )
如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )