题目内容
已知函数f(x)=ex-ax,g(x)=xf(x),设曲线y=g(x)在点(-1,g(-1))处的切线为l(e是
自然对数的底数).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a=1时,求曲线y=g(x)图象上与l平行的切线l′的方程,并判断l′与曲线y=f(x)是否存在公共点(若存在,请求出公共点的个数,若不存在,请说明理由).(参考数据:ln2=0.69…,ln3=1.09…)
自然对数的底数).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a=1时,求曲线y=g(x)图象上与l平行的切线l′的方程,并判断l′与曲线y=f(x)是否存在公共点(若存在,请求出公共点的个数,若不存在,请说明理由).(参考数据:ln2=0.69…,ln3=1.09…)
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,分类讨论,利用导数的正负,即可求f(x)的单调区间;
(Ⅱ)求出g′(-1)=2,由(x+1)ex-2x=2,可得x=-1或x=ln2,从而可得切线l′的方程;令h(x)=ex-x-(2x-ln22)=ex-3x+ln22,证明函数在(ln3,+∞)上单调递增,在(-∞,ln3)上单调递减,即可得出结论.
(Ⅱ)求出g′(-1)=2,由(x+1)ex-2x=2,可得x=-1或x=ln2,从而可得切线l′的方程;令h(x)=ex-x-(2x-ln22)=ex-3x+ln22,证明函数在(ln3,+∞)上单调递增,在(-∞,ln3)上单调递减,即可得出结论.
解答:
解:(Ⅰ)∵f(x)=ex-ax,
∴f′(x)=ex-a,
∴a≤0时,f′(x)=ex-a>0,即函数在R上单调递增;
a>0时,f′(x)>0,可得x>lna,函数在(lna,+∞)上单调递增,在(-∞,lna)上单调递减;
(Ⅱ)当a=1时,g(x)=xf(x)=x(ex-x),
∴g′(x)=(x+1)ex-2x,
∴g′(-1)=2,
由(x+1)ex-2x=2,可得x=-1或x=ln2,
x=ln2时,g(x)=ln2(2-ln2),
∴切线l′的方程为y-ln2(2-ln2)=2(x-ln2),即y=2x-ln22,
令h(x)=ex-x-(2x-ln22)=ex-3x+ln22,则h′(x)=ex-3,
∴函数在(ln3,+∞)上单调递增,在(-∞,ln3)上单调递减,
∴x=ln3时,函数取得最大值h(ln3)=3-3ln3+ln22>0,
∴h(x)=0有两解,
∴l′与曲线y=f(x)有两个公共点.
∴f′(x)=ex-a,
∴a≤0时,f′(x)=ex-a>0,即函数在R上单调递增;
a>0时,f′(x)>0,可得x>lna,函数在(lna,+∞)上单调递增,在(-∞,lna)上单调递减;
(Ⅱ)当a=1时,g(x)=xf(x)=x(ex-x),
∴g′(x)=(x+1)ex-2x,
∴g′(-1)=2,
由(x+1)ex-2x=2,可得x=-1或x=ln2,
x=ln2时,g(x)=ln2(2-ln2),
∴切线l′的方程为y-ln2(2-ln2)=2(x-ln2),即y=2x-ln22,
令h(x)=ex-x-(2x-ln22)=ex-3x+ln22,则h′(x)=ex-3,
∴函数在(ln3,+∞)上单调递增,在(-∞,ln3)上单调递减,
∴x=ln3时,函数取得最大值h(ln3)=3-3ln3+ln22>0,
∴h(x)=0有两解,
∴l′与曲线y=f(x)有两个公共点.
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,正确构造函数,确定函数的单调性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某学校推荐甲、乙、丙、丁4名同学参加A、B、C三所大学的自主招生考试.每名同学只推荐一所大学,每所大学至少推荐一名.则不推荐甲同学到A大学的推荐方案有( )
| A、24种 | B、48种 |
| C、54种 | D、60种 |
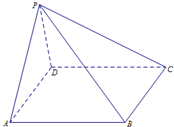 已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,且∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积是( )
已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,且∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积是( )